It’s time to talk about interest rates, discount rates and time value of money. Three inter related core concepts in Finance that lead to a number of interesting applications.
Compounding
Let’s go back to a simple investment. We put in a 100 dollars in our friendly neighborhood bank account. As long as the money stays in the account for one full year, it will grow to 110 dollars, for a net return of 10%.
What if the money stays in the account for two years or even more? Let’s assume that the day you invest the money in the bank, a wormhole (space time anomaly, dimensional gateway, a doorway to another universe) opens from nowhere, swallows you and spits you back in your home world after 100 years in hibernation. Amazingly the bank and your account have survived your unplanned absence and the bank has been paying you interest all of these years. Guess what: YOU ARE RICH! You go to the bank and find out that your account contains exactly one million three hundred and seventy eight thousand and sixty one dollars and twenty three cents. In order to make sure that there is no mistake or miscalculations on the bank statement, you decide to run the numbers yourself. Here are the details & the assumptions the bank made in calculating your balance.
- Pays interest every year on 31st December on the balance in your account on 1st of January of that year.
- Adds interest to your balance on 31st December.

Compounding formula – short cut
We can carry this on for the next 90 years. Instead of making 90 additional calculations, there is a shortcut to help us save time and space. Do you see a pattern above? If not, let’s see if we can make it more obvious. Our objective is to avoid the repetitive calculations and reduce 100 years of number crunching to one simple formula.
We already know the following:
- 1st year end balance = Principal * (1 + 10%)
- 2nd year end balance = 1st year end balance * (1 + 10%)
- 3rd year end balance = 2nd year end balance * (1 + 10%)
- 4th year end balance = 3rd year end balance * (1 + 10%)
- (and so on…..)
To simplify and calculate “4th year end balance”, we need to keep on substituting all definitions till we are down to something that just has “original balance” and (1 + 10%). The substitution sequence is as follows:
Balance at the end of the 4th year = Balance at end of 3rd year * (1 + 10%) = Balance at end of 2nd year * (1 + 10%) * (1 + 10%) = Balance at end of 1st year * (1 + 10%) * (1 + 10%) * (1 + 10%) = Principal * (1 + 10%) * (1 + 10%) * (1 + 10%) * (1 + 10%) = Principal * (1 + 10%) ^ 4
Read the “^” sign as “raised to the power of” or “to the power of”. Even simple calculators and spreadsheet programs have a function that can allow you to calculate “(1 + 10%) raised to the power 4”. When you run the numbers, you will find that the answer is 1.46.
Now we come to the difficult part. How would you calculate the growth in your account at 10% interest for the next 100 years.
The answer is “Principal * (1 + 10%) ^ 100”. The number, as we already know, is 1.378 Million dollars.
We call this approach compounding or compound interest because this year’s interest is next year’s principal.
Time Value of Money
Let’s look at another example that takes a different angle. My friendly bank manager has offered me a guaranteed return of 10% on anything that I put in my account as long as that amount stays in the account for one full year. I know that I would need 11,000 dollars at the end of one year to buy myself something, anything, everything. What do I need to put in today, that the X amount (principal) @ 10% a year will grow to 11,000 at the end of year one?
Interesting question. Let’s take another look at the work we did above.
We already know that at 10%, a dollar today grows to
1 * (1+ 10%) = 1.1
What we need to know is what principal today will grow to 11,000 dollars at 10% a year. So the above equation becomes
Principal * (1 + 10%) = 11,000
Or using basic manipulation
Principal = 11,000 / (1 + 10%) = 10,000
What this says is that to have 11,000 dollars one year from now, we need 10,000 dollars at an interest rate of 10% today.
What about 11,000 dollars two or even three years from now?
Well, we already know that a dollar at 10% in two years will grow to
1 * (1 + 10) ^ 2 = 1.21
Taking the approach used above
Principal * (1 + 10%) ^ 2 = 11,000
Principal = 11,000 / (1 + 10%) ^ 2 = 11,000 / 1.21 = 9,090
So what does this means? The 11,000 dollars we need two years from now are valued 9,090 dollars today.
Discounting
What we have just done above is called discounting. We are adjusting the value of a payment that we will receive at a point in future. This adjustment is called discounting. Therefore, we are discounting back a future value to bring it to its present value. The discount rate is the rate we use to adjust the future payment.
The idea behind discounting or compounding is also known as time value of money. Since a dollar at a fixed interest rate will grow in any bank account at that certain rate, if it is invested in an alternate opportunity, it should at least earn that rate from the other alternative to even consider the alternative worth thinking about. Discounting adjusts future payments, investment returns and even return of principal on this basis. The idea is that if you fail to earn the discount rate, you have actually lost money, since any bank, would at least have given you the discount rate as return for depositing your money with them. Anything less than that would mean that you have not put your money to its best use.
Present & Future Values
When we calculate the value of future payments today, we are doing a present value calculation. If we try to value what a stream of future payments is valued at today (the value of receiving 1,000 dollars a month for the next 36 months ), it is also a present value calculation. When we calculate the value of anything in the future we do a future value calculation. If we try to determine what a stream of future payments will be worth at some point in the future (the value of paying 1,000 dollars a month for 36 months, 36 months from today), it is also a future value calculation.
The analysis of any investment generally requires discounting (present valuing or pv’ing) two streams of numbers.
The first is the amount invested. If you put in a 1,000 dollars in an investment, every year for the next 5 years, that investment is worth the present value of five payments of 1,000 dollars each, one year apart.
Worth of investment today (Present Value of Investment) =
PV of $1000 (1 year from now) + PV of $1000 (2 years from now + ….+ PV of $1000 (5 years from now)
The second is the promised return. If in return for this investment you would receive 5,000 dollars in each six years and seven years from now, is it a good investment?
The value of these two payments is equal to the present value of two payments of 5,000, spread over two years and starting five years from now (year six and year seven).
Value of stream of return today (Present Value of Return) = PV of $5000 ( 6 years from now) + PV of $5000 ( 7 years from now)
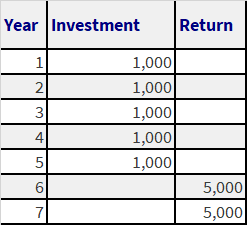
A positive NPV denotes that at a certain cost of capital the returns or inflows from an investment opportunity outweigh the outflows or costs of investment, and vice versa. Obviously, when comparing various alternatives available for investment, the option with the most positive NPV or least negative NPV will be favoured or chosen. The ensuing discussion on “Present Value in Action” will make these concepts clear.The Net Present Value (NPV) of this opportunity is the present value of the return (inflows) less the present value of the investment stream (outflows).
Examples
Example # 1
1) Natasha has a chance to invest in a project, Ventures, Inc. that will pay her $100 in year 1, and $200 in year 2.How much is she willing to pay for this opportunity? Assume an annual discount rate of 10%.
Solution: She will be willing to pay an amount that is equal to the present value of this stream of payments. To calculate the present value, you need to divide the payment by its respective discount factor.
- Discount factor for year n = (1 + [discount rate])^n
- Discount rate given=10%
Therefore:

Total PV = Sum of PVs of payments = $ 256.20
Hence, she would be willing to pay $256.2 for this opportunity.
Example # 2
Zia wants to lease a car for 3 years. The car dealer has given him two payment options to choose from:

Which payment option should he choose? (Assume an annual discount rate of 10%)
Solution:
In order to decide which payment to choose from, he would need to calculate the PV of the payment stream, and look at which costs him the least. Using the following:
- Discount rate= 10%
- Discount factor for year n = (1 + [discount rate])^n
- PV of payment in year n = [payment in year n] / [discount factor for year n]
- Total PV = Sum of PVs of payments
Present value of payment stream for option 1

PV of payment stream for option 1 = $ 5,547.5
Present Value of payment stream for option 2

PV of payment stream for option 2=$ 6,783.3
Conclusion: Hence he should choose option 1 as it costs him less than option 2.
Example # 3
Zareena’s firm, Tots and Toys, Inc. offers her an investment plan that requires 10 yearly payments of $1000, starting from today. The plan promises an annual return of 8% on her investment. The money will be available to her at the end of 10 years (no withdrawls are allowed before that time.) What amount will she get at the end of 10 years?
Solution: The question requires you to find the future value (FV) of the stream of payments. The rate given is 8%.
In order to find the FV, you need to multiply each amount by its respective FV factor, and then sum the results.
Discount rate given = 8%
FV factor for year N = (1 + [discount rate])^(10 – N)
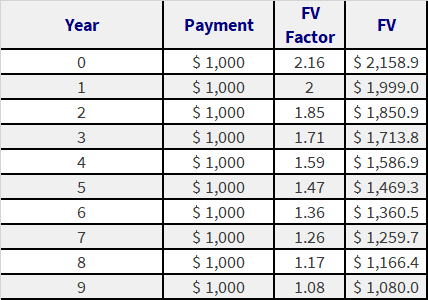
Amount at the end of 10 years = Sum of FV’s of payment = $15,645.5
Example # 4
Its Jan 1st, 2000 and WeGotItAll, Inc., your brand-new start-up, is in dire need of cash. You decide to take a loan of $100,000 from the bank. Interest on the loan will accrue at the rate of 10% and the bank requires that you pay back $10,000, on Jan 1st, every year starting 5 years from now, and therest of the amount on Jan 1st, 2010. How much is this final amount?
Solution:
In order to calculate the amount, you need to calculate the future value of the stream of cash flow, using 10% as your discount rate.
Using:
- Amount borrowed = $ 100,000
- Interest rate = 10%
- Annual payback amount $ 10,000 (starting from year 5)
- Interest for year = [Amt at year beginning] * [Interest rate]
- Amount at year end = [Amount at year beginning] + [Interest for year]
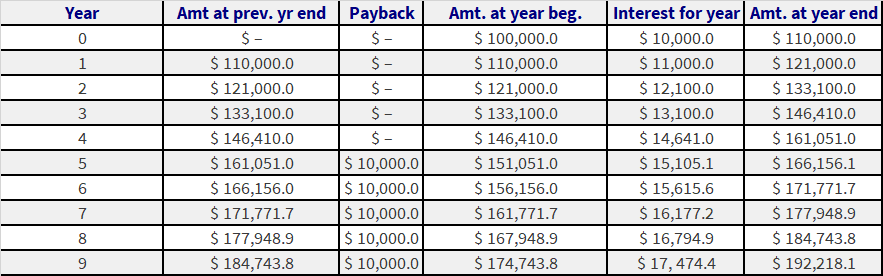
Hence you would need to pay back $192,218.1 on Jan 1st, 2010.
Example # 5
You have just sold your start-up for a $100 million, and your friend comes up to you asking you to invest in his new start-up. He says he needs $100,000 now, and will require a further $50,000 each in years 1 and 2. For your investment, he is willing to give you 30% of his company which he expects to sell for $80 million in year 5. What is the NPV of this opportunity?
Assume a discount rate of 30% for this risky investment.
The first thing to do is chalk out the cash flows, including both the inflows and the outflows:

Using:
- Discount rate = 30%
- Discount factor for year n = (1 + [discount rate])^n
- PV of cash flow in year n = [payment in year n] / [discount factor for year n]
- NPV = Sum of the PV’s of the cash flows

Example # 6
Gabes is the CFO of eBizz, Inc. His company has a beta of 2, and has no debt on its books. Due to its rapid growth Gabes is in dire need of cash and decides to increase his company’s leverage to 25%. How does that affect his cost of capital? (Assume that taking on debt does not change your beta)
Ignore the tax effects of debt.
Assume the following:
- Risk free rate= 6%
- Market risk premium = 8%
- Cost of debt = 10%
Solution
Cost of equity = [risk free rate] + Beta * [market risk premium]
Therefore:
Cost of equity = 6% + 2*(8%) = 22.00%
This is also your initial cost of capital, since you had no debt on your books.
Now, Cost of capital = [% of debt] * [cost of debt] + [% of equity] * [cost of equity]
We know that leverage has been increased to 25%.
This means that:
Debt/Equity = 25% = ¼
This means that now his company is 1/5th debt and 4/5 equity.
Therefore:
Cost of capital = (20% * 10%) + (80% * 22%) = 19.60%
Hence issuing debt has lowered his cost of capital.

Comments are closed.