In this post, we look at how to price interest rate caps and floors using caplets and floorlets and Black’s formula.
Caps and Floors
The most commonly used options in the swaps market are caps and floors. A cap is a call on the rates where the payoff depends on Max (LIBOR – Strike, 0). A floor is a put on the rates where the payoff depends on Max (Strike-LIBOR, 0).
Interest Rate Cap Pricing
A cap may be considered as a portfolio of caplets on the underlying asset which is the LIBOR. The value of the caplet may be derived using Black’s Formula. The value of a caplet which resets at time ti and payoffs at time ti+1 is:
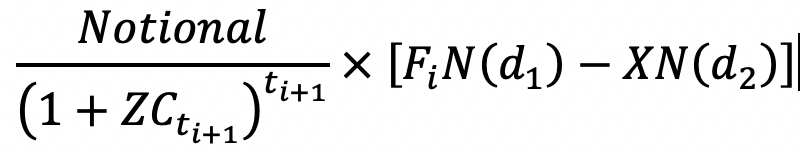
Where [Fi N(d1)-XN(d2)] is known as the forward premium, X is the Strike, Fi is the forward rate at time 0 for the period between ti and ti+1 and σti is the volatility of this forward interest rate.
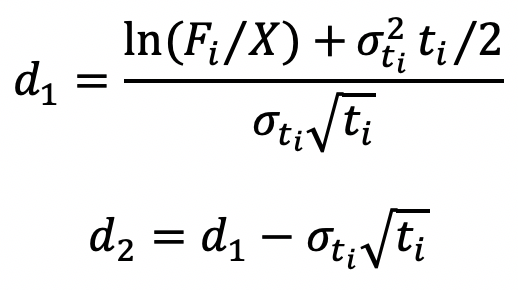
This is illustrated below for a 4 year cap on a 1 year Inter-bank offer rate with a strike of 12.5%. The annualized constant volatility is 3.13%. The valuation date is 31/5/2010 and the payment frequency is annual. The notional amount is 100,000.
| Period Start (i) | Period End (i+1) | ti | ti+1 | ZCti+1 | Fi | d1 | d2 | Forward Premium | Value of Caplet |
| 01/01/10 | 01/01/11 | n/a | 0.59 | 12.150% | 12.150% | n/a | n/a | – | – |
| 01/01/11 | 01/01/12 | 0.59 | 1.59 | 12.225% | 12.269% | -0.76 | -0.79 | 37.26 | 31.02 |
| 01/01/12 | 01/01/13 | 1.59 | 2.59 | 12.349% | 12.583% | 0.19 | 0.15 | 241.75 | 178.77 |
| 01/01/13 | 01/01/14 | 2.59 | 3.59 | 12.418% | 12.595% | 0.18 | 0.12 | 302.29 | 198.53 |
| Price of Cap | 408.33 |
The calculation of d1 and d2 are based on the duration at the start of the period, i.e. ti. Therefore for the first row, we see that these values cannot be calculated. The forward premium in this case is simply equal to the payoff i.e. Max(Fi-X,0)*Notional*∆t/365 =max(12.15%-12.5%,0)*100000*0.59=0
For the other rows as d1 and d2 can be calculated the Forward Premium from Black’s formula will be used.
The price of the cap is the sum of the values of the caplets, which are the present values of the forward premiums.
Interest Rate Floor Pricing
An interest rate floor may be considered as a portfolio of floorlets on the underlying asset which is the LIBOR. The value of the floorlet may be derived using Black’s Formula. The value of a caplet which resets at time ti and payoffs at time ti+1 is:
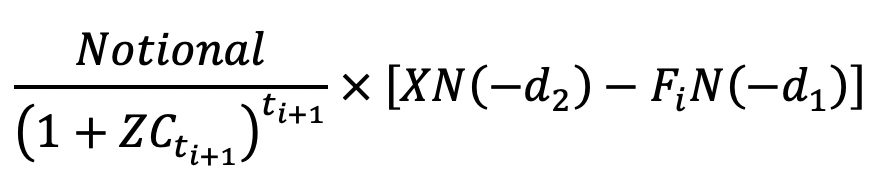
Where [XN(-d2)-Fi N(-d1)]is the forward premium. d1 and d2 are as given above. The value of a 4 year interest rate floor with the strike, volatility, notional, maturity and payment frequency the same as for the cap above is illustrated below:
| Period Start (i) | Period End (i+1) | ti | ti+1 | ZCti+1 | Fi |
| 01/01/2010 | 01/01/2011 | n/a | 0.59 | 12.150% | 12.150% |
| 01/01/2011 | 01/01/2012 | 0.59 | 1.59 | 12.225% | 12.269% |
| 01/01/2012 | 01/01/2013 | 1.59 | 2.59 | 12.349% | 12.583% |
| 01/01/2013 | 01/01/2014 | 2.59 | 3.59 | 12.418% | 12.595% |
| d1 | d2 | Forward Premium | Value of Floorlet |
| n/a | n/a | 206.16 | 192.70 |
| -0.76 | – 0.79 | 268.02 | 223.14 |
| 0.19 | 0.15 | 158.39 | 117.12 |
| 0.18 | 0.12 | 207.47 | 136.26 |
| Price of Floor | 669.22 |
Again it may be noted that the calculation of d1 and d2 are based on the duration at the start of the period, i.e. ti. Therefore for the first row we see that these values cannot be calculated. The forward premium in this case is simply equal to the payoff i.e. Max(X-Fi,0) * Notional * ∆t/365 = max(12.5%-12.15%,0)*100000*0.59=206.16
For the other rows as d1 and d2 can be calculated the Forward Premium from Black’s formula will be used.
The price of the interest rate floor is the sum of the values of the floorlets, which are the present values of the forward premiums.
Cap Floor Parity
The cap floor parity says that being long a cap and short a floor with the same strike is equivalent to paying the fixed leg in the swap where the fixed rate is equal to the strike rate.
In other words, Cap – Floor = Swap.
From the pricing examples above, we see that this value is
408.33-669.22 =-260.89.
Calculating an interest rate swap, with fixed rate equal to the strike of 12.5%, notional =100,000, payment frequency = annual and payment dates similar to that of the cap and floor above we see that the value of the swap is as follows:
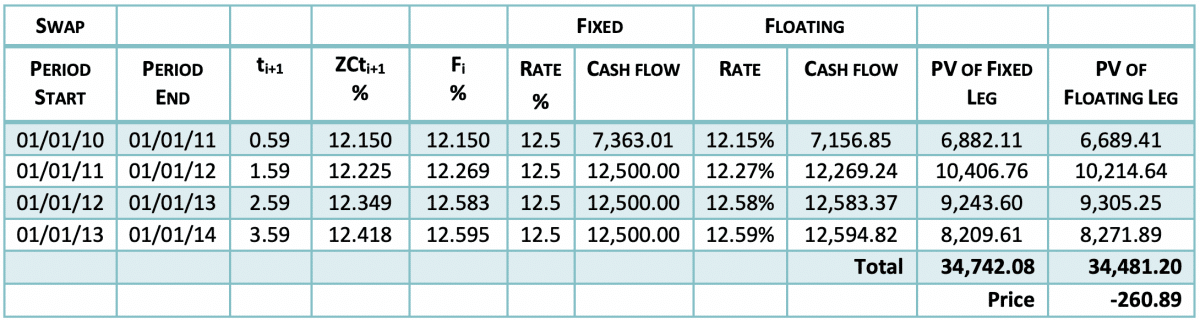
As we can see the value of the IRS is equal to the value of the Cap minus the value of the Floor.
For a formula reference, please see the following link

Comments are closed.