Pricing Interest Rate Swaps – Terminology and Notation

2 mins read

Session One

Definitions

Cash flows

The key to pricing or valuing any instrument is to estimate the cash flows of the instrument and discount each cash flow using an appropriate rate of interest.

Cash flow is simply the cash that is expected to be received each period from an investment. For a bond this includes coupon and principal payments; for an interest rate swap this would include fixed or floating rate coupon payments, etc. In order to price an instrument is it important to project the amount and timing of cash flows. For non-callable Treasury bonds the timing and amount of the cash flows are known in advance. For other instruments there may be greater difficulty in projecting cash flows. Some of the reasons for this difficult include:

1. The buyer or seller of the instrument may have the option to change the contractual due date(s) of the payments
2. The coupon payment may be based on a floating rate that is reset periodically based on some reference rate such as the LIBOR

A key factor in determining the projected cash flows is the level of interest rates in the future. It will be discerned in relation to the instruments coupon rate to determine whether the buyer or seller will exercise the option to change contractual payment dates. It will also be used to discern what the coupon payment will be for floating rate instruments whose payments are dependent on the level of in the future of some reference rate.

Discounting Cash flows

Once the cash flow is estimated, it is then important to determine the appropriate interest rate to use to discount the cash flows in order to value or price the instrument. The value of the instrument is the present value of each cash flow.

Spot Rates

A t-period spot rate is the per period rate of interest that can be earned on an investment made today (Time 0) which would be repaid with interest on a specified date in the future (Time t). Another name used for a spot rate is a zero coupon rate.

Forward Rates

Assume you are choosing between buying a 6-month zero coupon bond and then reinvesting the money in another 6-month zero coupon bond OR buying a one year zero coupon bond. Today you know the rates on the 6 month and 1 year bonds, but you are uncertain about the future six month rate.

The forward rate is the rate on the future six month bond that would make you indifferent between the two options. It is the rate of interest that would be applicable from one point in time in the future to another point in time in the future. These rates are implicit in the current quoted spot rates. Typically forward interest rates are expressed as single period rates but they could also be applied to several time periods. The rates are inferred from available data.

The difference between spot (s_t) and forward rates (f_t-I,t) is illustrated in the time line below:

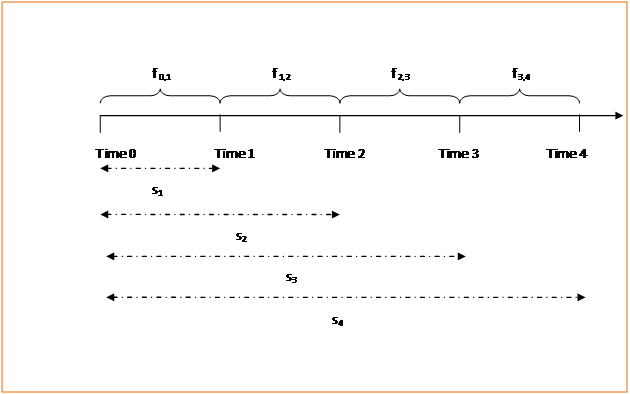
The line segments appearing in the illustration above below the timeline represent the lengths of time over which the various spot rates, st, are applicable. The spot rates of interest always refer to a time interval beginning now, i.e. at Time 0. The lengths of time appearing above the timeline indicate the lengths of time over which the forward rates are applicable. As can be seen above and as mentioned earlier forward rates are single period rates.