Sharpe Ratio
The Sharpe Ratio measures total risk-adjusted return. The value specifically is the ratio of excess return over the risk free rate to the riskiness of the investment as given by the volatility of investment’s returns i.e. it measures the return per unit of the investment’s total (systemic + specific) risk.
The formula for the Sharpe Ratio is given below:
Where
RI =Scaled holding period return of investment I. The return is scaled to one year. The calculation methodology for scaled holding period return has been discussed in the following post:
Market Risk Metrics – Holding Period Return
Rf = Annualized risk free rate of return.
?I = Annualized volatility
For example, a Sharpe Ratio of 4 indicates that the underlying investment has earned an excess return over the risk free rate four times the level of risk that it adds. A negative Sharpe ratio indicates that the underlying investment has performed even worse than a risk free security on a risk adjusted basis.
The step by step methodology for Sharpe’s Ratio is given below. We start off first with the process for calculating the denominator, i.e. the annualized volatility in EXCEL:
First obtain the time series price data over the given period of analysis. This has been done for our sample stock ABC:
Next, calculate the daily return time series from the price data. The daily returns are calculated by taking the natural logarithm of the ratio of successive (consecutive) prices:
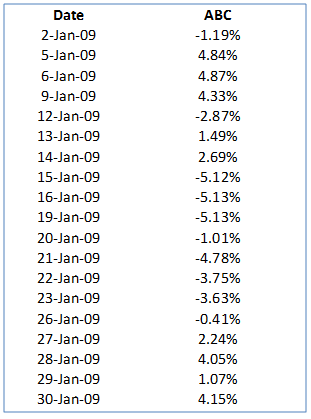
The resulting return series is given below:
Then calculate the standard deviation of the return series using the formula below:
Where
Xi= rate of return of the investment
? = average of the rates of return
n = sample size
This may be calculated in EXCEL using the STDEV() function applied to the arrange of stock returns as follows:
The daily volatility of stock ABC’s returns works out to 3.76%.
Once the daily volatility figure has been obtained it has to be annualized in order to be used in the Sharpe Ratio formula. This is done by applying the following formula (we assume 252 trading days in a year):
The annualized volatility for stock ABC’s returns works out to 59.68%.
As mentioned earlier the scaled holding period return was calculated in an earlier post for stock ABC. The scaled holding period return worked out to -40.59%.
Assuming a risk free rate of return of 12%, the Sharpe Ratio for stock ABC is calculated as follows:
Sharpe Ratio for Stock ABC = (-40.59%-12%)/59.68% = -0.88
This means that over the period of analysis stock ABC has performed even worse than a risk free security on a risk adjusted basis.
Treynor Ratio
Like the Sharpe Ratio, the Treynor Ratio is a risk-adjusted measure. However whereas the Sharpe Ratio measures excess return of the investment over risk free return per unit of total risk; the Treynor ratio measures the excess return per unit of risk in relation to the market, i.e. per unit of systematic risk. It is given by the following formula:
Where
RI =Scaled holding period return of investment I. The return is scaled to one year. The calculation methodology for scaled holding period return has been discussed in the following post:
Market Risk Metrics – Holding Period Return
Rf = Annualized risk free rate of return.
?I = Beta of the investment with respect to a well diversified broad market index. The calculation methodology for beta has been discussed in the following post:
Market Risk Metrics – Beta with respect to market indices
The Treynor Ratio is generally used to compare well diversified portfolios. However it may be used here to compare investments which have similar betas, i.e. it is useful when reviewing investments within the same systematic-risk-defined peer group.
A high positive Treynor Ratio shows that the investment has added value in relation to its (scaled-to-market) risk. A negative ratio indicates that the investment has performed worse than a risk free instrument.
We use our sample stock ABC to illustrate the calculation of the Treynor ratio. Scaled holding period returns for the Stock ABC as mentioned earlier is -40.59%. The risk free rate is 12% and beta for stock ABC as calculated in an earlier post is 1.20. The Treynor ratio works out to:
Treynor Ratio for Stock ABC = (-40.59%-12%)/1.20 = -0.44
Stock ABC has a negative Treynor ratio indicating that its performance has been worse than a risk free security.
Like this post – check out the new book – Portfolio Optimization Models in Excel, Revised Edition – 227 pages, Excel templates and dataset included.


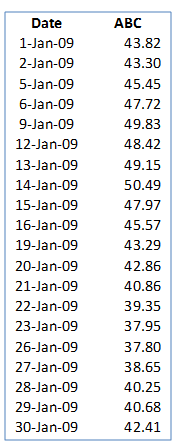
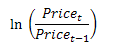
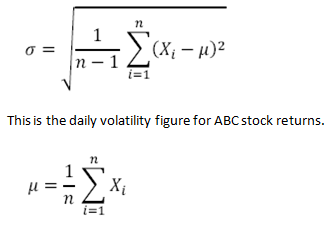


Canadian Investor: It’s true that countries can go into long denciles leading to poor stock market returns. It’s also true that countries can go into periods of high inflation which are devastating for real bond returns. Unless one can predict the future, the important question is what are the best guesses of expected returns and volatilities. I can’t do much to help people who get scared and cash out their investments in their entirety, but life events rarely require a full cash-out. Most life events can be handled with a reserve of liquid assets (usually cash). Even bonds may be too volatile depending on a person’s situation. The Sharpe ratio doesn’t address this problem. The Sharpe ratio is indifferent to whether a portfolio is 100% stocks or 100% short-term government debt.