Addendum: How to conduct a Principal Component Analysis in EXCEL
There are a couple of problems that the user may face after running the Solver function in EXCEL for the Principal Component Analysis of treasury yield rates.
1. Dummy Values for the Eigenvector matrix
The seed values that are put in the eigenvector matrix have an impact on the calculation. The user must ensure that all the dummy values are not the same number such as all zero values because the Solver function will then return a #NUM! error. One way of handling this potential issue is to use EXCEL’s RAND() function to generate the dummy values within the matrix, then Copy and Paste Special the resulting numbers as Values over the matrix.
Run the solver function using this dummy data set.
2. Solver cannot find a feasible solution
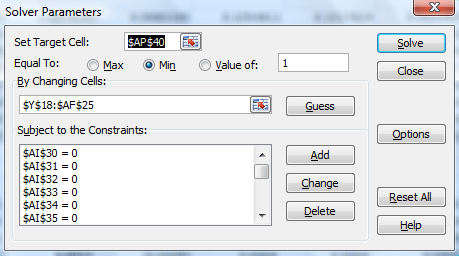
Because of the limitations of the solver function, it may return the message that it could not find a feasible solution. Some changes may be made within the solver function set up to enhance its capability such as, alternating between setting the target cell value to “Min” or “Value of =1”,
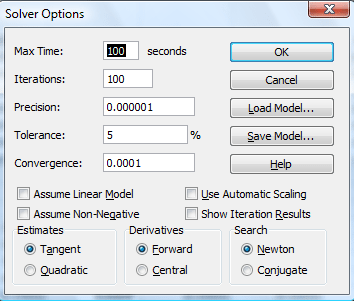
Or clicking on “Options” to go to advanced settings:
And increasing the number of iterations and/or reducing the tolerance level.
Despite these changes the message may continue to appear. Therefore some manual manipulation may be required in the worksheet after each Solver run.
Go to the results table:
Note that the ideal result would be for the Percentages (2nd row above) to appear in descending order, from largest to smallest, which is not the result obtained in the case above.
The percentages correspond to a given eigenvalue and eigenvector. We can see that the 5th eigenvalue has the highest percentage followed by the 2nd and 3rd then the 8th, 4th, 1st, 7thand finally the 6th.
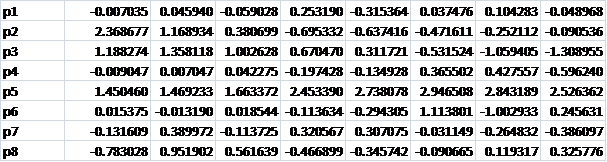
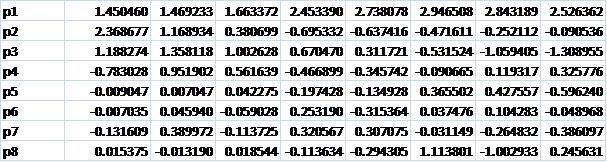
So we re-order the eigenvector matrix accordingly. Note: do not cut and paste the rows, to reorder, within the matrix as it will corrupt the worksheet. Instead copy and paste the values to a separate location on the sheet or to another sheet, reorder and then paste the reordered matrix back onto the matrix cells within the worksheet:
Eigen vector before re-ordering:
Eigen vector after re-ordering:
Rerun the solver function.
This process may need to be repeated a number of times. Note that at each stage keep the results of the solver run. Check the order of the percentages, rearrange the eigenvector matrix accordingly and rerun Solver. Continue with this process until you finally arrive at a feasible solution: