We will look at two methods to calculate the value at risk of bonds. There are two common challenges that arise in applying risk management concepts to individual bonds and bond portfolios within fixed income investment management:
a) How do you measure the risk of a newly issued bond that has no history of trading prices
b) How do you integrate the risk of a bond issued in a foreign currency into your default base currency.
Both questions have simple solutions that will use this two part case study to illustrate. In this post, we will focus on how to calculate the value at risk for new issues of bonds. In our next post, we will review how to calculate the value at risk for bonds that trade in foreign currencies.
Bond Risk Management Background

When it comes to bond risk management, Modified Duration is the primary measure that portfolio and investment managers use. This is a measure of interest rate sensitivity that tracks changes in bond prices because of changes in interest rates. Value at risk is a relatively new arrival to the scene and brings price volatility into the picture. However, a newly issued bond as well as an illiquid bond may have limited, thin or no trading data. In the absence of trade related price data, we look at other options.
One possible option is to identify the relevant interest rates for the bond in question. For example, to price a 10 year bond with no price history we can pick up the history of applicable 10 year rates and then use them to price the bond, assuming that future rates and price behavior will be similar to that witnessed in the past. When we apply historical rates we also assume constant maturity. This means that changes in the price of the bond are only on account of changes in interest rates and not because of a change in days to maturity of the bond.
We use the above concept to calculate the risk inherent in a single bond or a portfolio of bonds. For a quick refresher on value at risk see our earlier posts on from risk to value at risk.
Rate VaR or Price VaR?
If you have calculated value at risk before for equities and currencies, here is a quick question on how to calculate value at risk for bonds and fixed income instruments. Should you calculate value at risk using interest rates (Rate VaR) or bond prices (Price VaR)? Think about it if bonds don’t trade or are illiquid which one of the above two (rate vs. price VaR) is a better choice, is more representative of the risk inherent in your fixed income positions – interest rates or prices?
The answer should be clear.
The relevant risk measure is price value at risk since it reflects actual changes in prices. Rate VaR only reflects changes in interest rates or interest rate volatility but is not an accurate measure of value changes. (Why?).
A ten year bond reacts very differently to a 1% change in rates when compared to a 3 month treasury bill. If that doesn’t convince your audience, here is another argument. In general overnight rates have the highest volatility. What should be the likely change in the price of a treasury bill that only has one day to go? If you use rate VaR you will have an unreasonably high number. Even if rates double up, what would the impact of the new rates on one day of interest accrual? Hence, price VaR is the right choice.
This question rarely comes up but has been asked once or twice by board members. Risk committees, given all the attention bestowed on them after the London Whale crisis, are now more curious about the relationship between rate and price value at risk and its best to be prepared with easy to understand logic that can clear their confusion.
VaR model walkthrough
For our base case, we use a 10 year maturity bond. The Coupon is 9% with semi-annually payments. We also know the dates of settlement and maturity and yield to maturity (YTM). Calculate Duration with these parameters. The figure below shows the parameters:
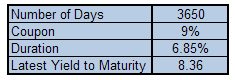
To build the model we will calculate interest rate value at risk (Rate VaR), bond price value at risk (Price VaR) as well as the delta normal approximation which translates rate VaR into price VaR by using modified duration.
To calculate the modified duration we use Excel’s modified formula. We also assume constant maturity which means that when we use historical bond prices to calculate price returns we assume that the maturity of the instrument remains the same. The two columns below (column D and E) reflect the historical yields for the bond in question as well as the change in those yields on a day to day basis.

Note that Yield to Maturity (YTM) used is 6.45% not 8.36%. 8.36% represents the most recent YTM that we use for calculating the Delta Normal valuation shortcut which we will cover later. Calculate the date of maturity column by adding ‘Number of days to maturity’ to the settlement date.
Finally, calculate the return series by taking the natural logarithm (LN) of two consecutive YTMs (YTM ahead divided by YTM behind).
Calculate Value at Risk for Bonds using Interest Rates – Rate VaR
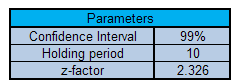
Once you have the return series for interest rates, rate VaR uses the EXCEL standard deviation function to calculate the volatility of rates and then apply the VaR parameters to calculate Value at Risk for the relevant interest rate.

Now calculate Rate VaR using the standard Value at risk formula. See refresher on value at risk if you are lost.

Calculate Value at Risk for Bonds using Prices – Price VaR
For bond Price VaR we use the same process with a few changes. Rather than using interest rates we use the Excel price formula to calculate new prices for each new interest rates. We apply the natural log to calculate the return series and then calculate the standard deviation on the return series. Plug the standard deviation into our VaR calculator to get our Price VaR estimate.
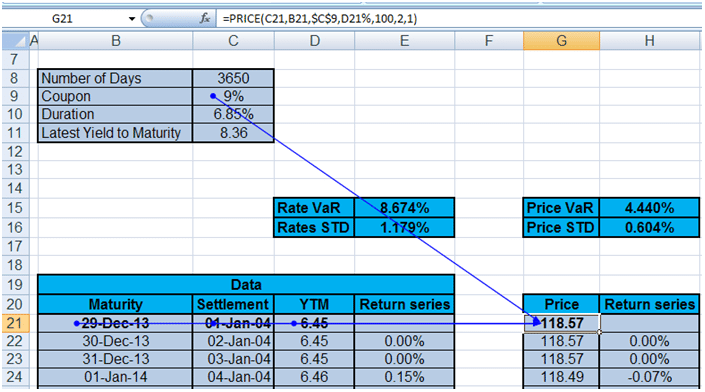
Comparing Rate VaR and Price VaR
Now that we have both Rate VaR and Price VaR let’s do a quick comparison.
For the 10 year bond with the default level of rate volatility, Rate VaR shows almost double the value at risk estimate. What happens when maturity drop from 10 years to 3 years while keeping volatility constant? The snapshot below shows the revised calculations for a three year bond.
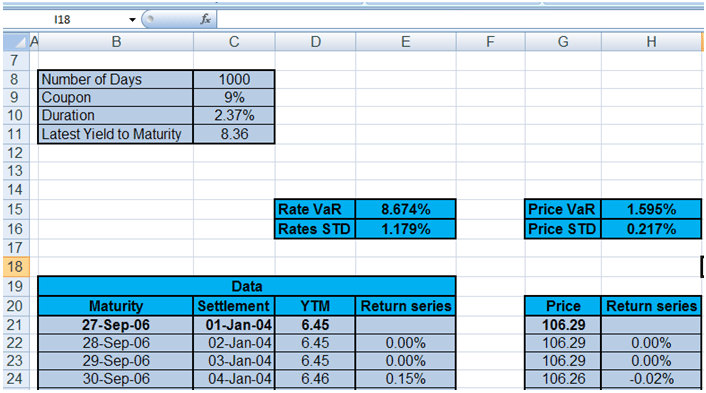
While Rate VaR doesn’t shift, Price VaR immediately reflects the impact of reduced maturity and modified duration
An Alternative approach to calculating Price VaR from Rate VaR: The Delta Normal Method
Delta normal method can be used to find an approximate value close to the value of Price VaR using rate VaR. The bond price function is expensive in terms of calculation power and if we can come up with a quick (but crude) approximation it can save us time on large multi position portfolios. The Delta Normal method is a shortcut method that delivers on that promise.
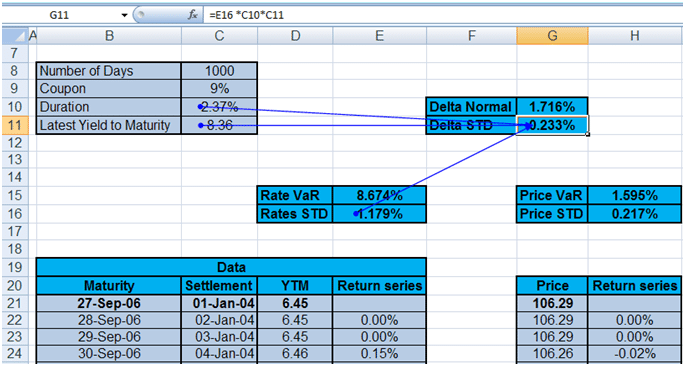
The revised standard deviation or volatility for the Delta Normal method multiplies the interest rate standard deviation with modified duration and the most recent YTM. We then plug in the revised Delta Normal standard deviation in our VaR calculator to get the new Delta Normal Value at Risk.
Delta Normal VaR= Delta std*z-factor of the specified confidence interval*square root of holding period.
While the fit is not perfect on account of the convexity approximation, it is a much better result than the original rate value at risk estimate. And you don’t have to use the bond pricing function.
