Active and passive investment management styles
How much value does a trader or investment manager bring to the table? In terms of alternates, an investor can simply invest in a market based index and let market performance dictate his returns. This has two benefits. First investing in the market index has no associated fees or costs other than the preset re-balancing every few weeks. Even if he opts for a managed market index based fund with fees, the level of fees charged for such products is significantly lower than that of an active investment fund manager.
Alternatively he can work with an active fund manager and come out ahead only if the fund manager is able to beat the market returns net of fees. An active fund manager adds value over the market by his research oriented sector allocation, security selection and market entry and exit decisions (timing). The best fund managers who can do this consistently (beat the market) year over year are rare. The simplest of performance test is the amount by which performance of an active fund manager surpasses that of the relevant benchmark index net of fees.
Index matching portfolio performances
Beating the Index is therefore a common challenge portfolio managers face. Matching performance with a passive or benchmark index on the upside, beating it on the downside. In some instances performance, compensation and market ranking is linked to the margin by which performance of an index is exceeded.
The Index matching problem can be addressed through two different approaches. Both approaches try and match portfolio metrics with those of the Index over the length of the observation period. For instance, assume that our index matching criteria includes risk, average expected return, Beta and alpha. The matching problem states that we should beat the index return with lower standard deviation, matching Beta and higher Alpha.
The optimization problem would then simple match the average portfolio values of these metrics with that of the Index across the investment horizon. In the simplistic approach this would be done as a matching problem over a single observation period. In the more advance approaches we will break the observation period into time bands and attempt to match portfolio metrics with the index metrics over each time period.
A third variation of the same problem is the spicing up investment returns challenge. An insurance company or a pension fund, may be bound by the nature of its liabilities portfolio to only invest in long duration bonds. The investment policy document may specify a threshold which must be invested in a bond portfolio. However the investment manager, may be willing to take some exposure to other asset classes as long as they reduce his overall volatility, increase return or help him with the index matching problem.
We will try work with one variation of the index matching problem in this post. The other two are left as a problem set submission for students in the course.
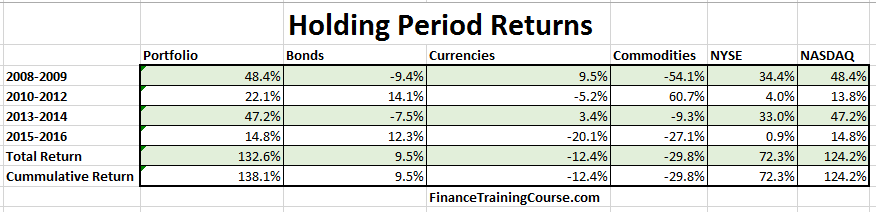
How do we evaluate the effectiveness of our solution. We use two different data set. A construction period data set and an evaluation period data set. The construction period data set is used to create and construct our portfolio recommendations using solver.
The evaluation period is different from the construction period and is used to independently validate the success or failure of the investment strategy by using a separate dataset from a different period. The idea is to see how formulations perform under conditions which were not part of the original optimization data set.
As Index matching problems increase in complexity it is important to understand how Solver reaches an optimal solution. Solver looks for local minimums and maximums in the problem space and sometimes given the dimensions involved in the solution it gets trapped in a rut or a hole that does not represent the optimal solution. It helps to attack optimization problems from alternate perspectives to avoid the trapped in a rut state. Rather than formulating a complex problem from the very beginning start with simple formulations and then incrementally add complexity. This step by step marginal approach has a higher chance of reaching an optimal solution than a single solution design that requires solver to attack multiple constraints in one go.
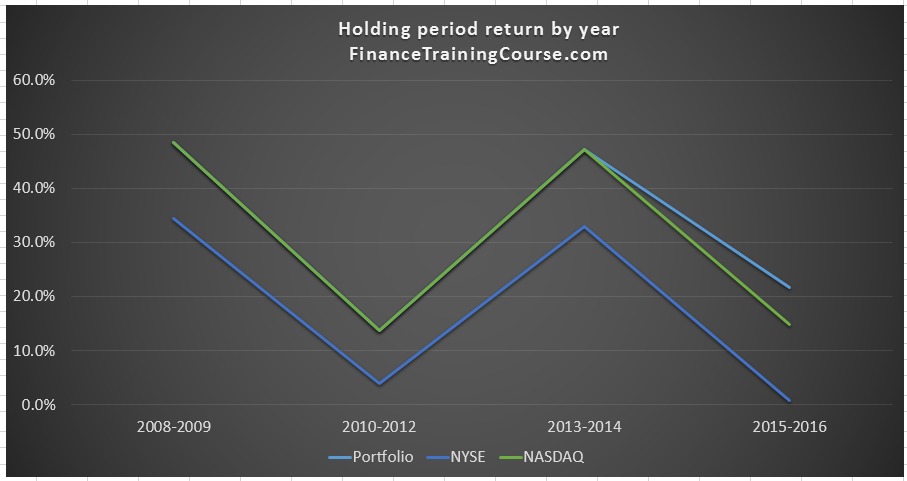
Here are the results of our first optimization challenge where we try and match the performance of our portfolio with NASDAQ.
Index matching portfolio – NASDAQ

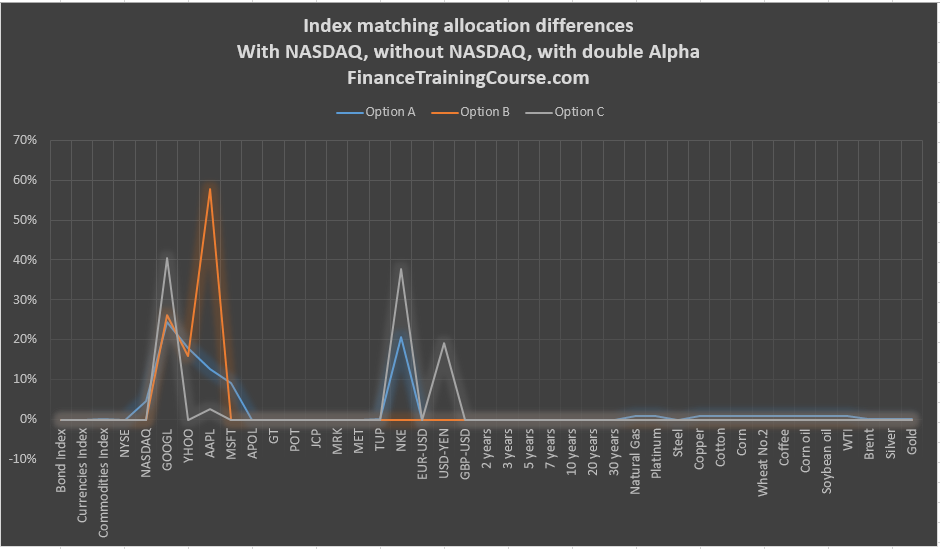
We match performance for NASDAQ using holding period returns for both single period as well as multiple time bands. We try three different variations. The first allows us to invest in NASDAQ as a security, the second without NASDAQ as a security and the third and final attempt that specifies Alpha of the portfolio be greater than double the expected Beta return.
The solver formulation for the final Alpha – Double Beta return variation is presented below.
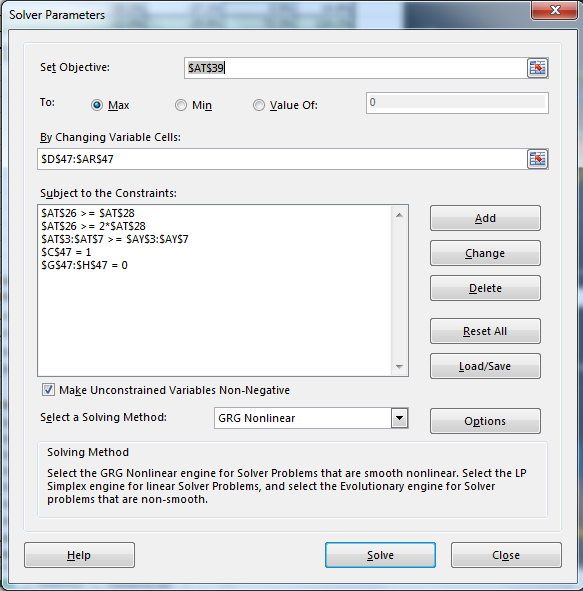
Here are the results from the Solver suggested solution for the three different variations.
Scenario 1 – With NASDAQ as an investment security.
We allow investment into the index as an investment security. While this defeats the purpose of the original index matching exercise we still wanted to see how much of the optimal portfolio would get allocated to NASDAQ by Solver.
Portfolio composition.
The surprise here is that NASDAQ allocation is limited to 5%. An invest in 5 tech stocks with a minor exposure to some bonds and commodity combination would have allowed you to beat NASDAQ in each of the holding period time bands specified by the problem set.

Holding period returns for scenario 1.
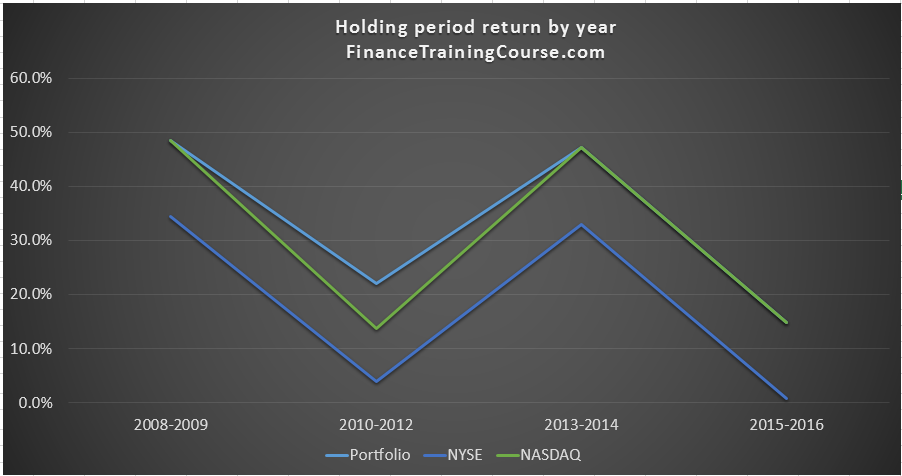

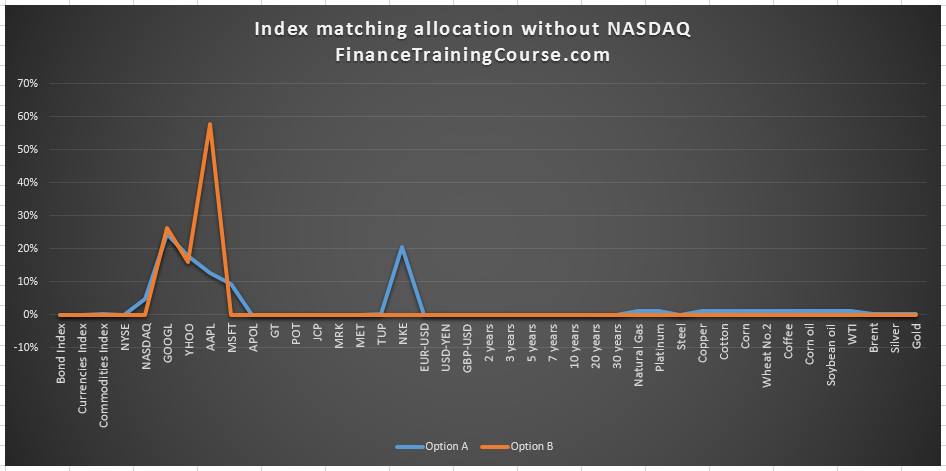
Scenario 2 – without NASDAQ as an investment security
Portfolio composition
We now remove NASDAQ as a possible investment. Solver reformulates the solution and limits it to just three securities that would have substantially out performed the Index over the initial two time bands.
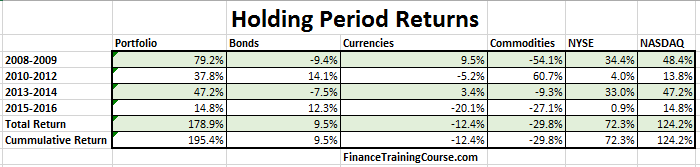
Holding period returns

Scenario 3 – With Alpha required to be double Beta return
Portfolio allocation
The objective here is to put some downside protection in place with the double Beta requirement.

Portfolio returns

How do the three different approaches fare in the post allocation evaluation period.
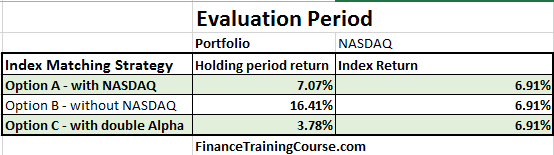
The real surprises are the results without NASDAQ and with double alpha variations. Two of the three variations beat the index using the evaluation period data set.
