Relationship between Spot and Forward Rates
The following formulas summarize the relationship between the spot and forward rates of interest:
ft-1,t = (1+st)t ÷ (1+st-1)t-1 – 1
or alternatively
As can be seen above the spot rates are geometric averages of the forward rates of interest.
Forward rates do not generally do a good job of actually predicting the future rate, but they do allow the investor to hedge. Taking our earlier example of choosing between buying a 6-month zero coupon bond and then reinvesting the money in another 6-month zero coupon bond OR buying a one year zero coupon bond. If the investor’s expectation of the future rate is less than the forward rate they are better off investing for the entire year and locking in the 6 month forward rate over the last 6 months now by buying a one year zero-coupon bond.
Short rates
These are single period future short term rates of interest that may arise over time. The difference between short rates and forward rates is that forward rates are implicit in the spot rates applying to different lengths of time and that for each future time period there exists at Time 0 one and only one applicable vector of forward rates. However, the future short term rate that may unfold one period later may or may not be equal to the forward rate that was calculated when we were at Time 0. In fact, there could be several possibilities of short rates for each future point in time and each possibility has a different probability of occurrence attached to it. These probabilities are consistent with the term structure of spot and forward rates that exist at Time 0.
Yield to Maturity
The yield to maturity or YTM is another type of interest rate. For zero-coupon bonds that are bonds that have only a single cash flow, the YTM will equal the spot rate. For coupon bearing bonds on the other hand which may have several payments during their term the YTM will depend on the spot rates that are associated with each individual cash flow. Alternatively, a coupon bearing bond may be thought of as a collection of zero-coupon bonds with each cash flow valued as a separate zero-coupon bond using a different spot rate of interest (depending on the tenor of the cash flow). The YTM will depend on the entire collection of spot rates used to value all the cash flows of the bond.
The YTM may be thought of as a complex weighted average of the spot rates on interest, where the weights depend on the pattern of cash flows that are due on the bond over its life.
To solve for YTM we are solving for the interest rate (r) in the bond valuation formula:
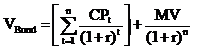
Where CPt is the coupon payment at time t and MV is the maturity value at time n (i.e. at maturity).
We cannot solve for r algebraically, only by trial and error or by using a financial calculator or excel.
Term structure of interest rates
The term structure of interest rates illustrates the level of interest rates by maturity on instruments of a similar credit risk.

The most commonly investigated and used term structure is the treasury yield curve. Treasuries are used since they are:
- Considered free of default, and therefore differ only in maturity
- The benchmark used to set base rates
- Extremely liquid

Comments are closed.