This section reviews the following Asset Liability Management (ALM) tools:
- Price Sensitive Gap
- Liquidity Gap
- Net Interest Income (NII) at Risk
- Duration Gap Analysis
It also looks at a couple of ALM applications with respect to banks and insurance companies that illustrate immunization and portfolio dedication respectively.
Asset Liability Management Tool – Price Sensitive Gap
The first Asset Liability Management Tool that we will look at is the Price Sensitive Gap report. The report evaluates the impact on the economic value of balance sheet items of shifts in a given term structure.
Step 1: Slot each asset and liability item of the balance sheet into their respective maturity buckets.
Step2: Calculate the marked to market value of each item on the revaluation date. This is will be denoted as the initial market value.
Step3: Recalculate a new marked to market value assuming shifts in the underlying term structure.
Step4: Calculate the difference between the initial and new market values (and the % change in the market value) to assess the gain or loss resulting from a shift in the term structure.
Asset Liability Management Tool – Liquidity Gap
The liquidity gap report which evaluates the liquidity gap and assesses the overall concentration of assets and liabilities across the maturity buckets.
The methodology followed is similar to rate sensitive gap however, here the focus is on liquid assets and liabilities rather than rate sensitive assets and liabilities.
Asset Liability Management Tool – Net Interest Income (NII) at Risk
The NII at risk report shows the impact of interest rate shocks on cumulative gaps for on-balance sheet and off-balance sheet items for different maturities. These gaps are as calculated for the Rate Sensitive report.
Asset Liability Management Tool – Duration Gap Analysis
The vulnerability of an institution towards the adverse movements of the interest rate can be gauged by using the duration GAP analysis. This is carried out using the following procedure:
Step 1: Identify Interest rate sensitive assets and liabilities. Additionally, non – interest rate bearing items can also be included in the calculation.
Step 2: Calculate the MTM value for all the rate sensitive assets.
Step 3: Calculate the MTM value for all the rate sensitive liabilities.
Step 4: Calculate the duration for each asset and liability of the on-balance sheet portfolio. This is calculated using Macaulay Duration.
Step 5: Calculate the aggregate weighted average duration of assets and liabilities.
- Weighted Average Duration of Assets (DA) = åWaDa
- Weighted Average Duration of Liabilities (DL) = åWlDl
Where,
W a = market value of the asset ‘a'(MTM) divided by market value of all the assets (Net MTM)
W l = market value of the liability ‘l'(MTM) divided by the market value of all the liabilities (Net MTM)
Da = duration of asset ‘a’
Dl = duration of liability ‘l’
Step 6: Calculate the duration GAP using the following formula:
DGAP = DA – DL * MVL/MVA
Where,
DA is the weighted average duration of assets,
DL is the weighted average duration of liabilities,
MVL is the total MTM of liabilities,
MVA is the total MTM of assets.
Step 7: Calculate the change in the market value of equity for a Di % rise in interest rates.
This is approximated using the following formula:
DMVE @ (-DGAP) * Di * MVA / (1 + y)
Where,
Di = The change in the interest rate,
y = The effective yield to maturity of all the assets.
ALM Applications – Bank
The portfolio & interest rate environment
Customer A deposits 100,000 in a bank’s one-year term deposit account that pays 10% per annum. This amount is guaranteed by the bank. At the end of the year (i.e. on 8th July 2011) the customer will receive 110,000 from the bank.
The bank invests this amount in its entirety on 8th July 2010 in coupon bearing instrument will the following characteristics:
| Face Value | 100 |
| Coupon | 10% |
| YTM | 12% |
| Frequency | 2 |
| Settlement date | 8-Jul-10 |
| Maturity date | 8-Jul-15 |
| Coupons reinvested at | 12% |
| Price on settlement date | 92.64 |
| Price one year later (assuming same YTM) | 93.79 |
The bank reinvests all coupons and will send the bonds at the end of the year to meets its obligations.
As mentioned above the full amount of deposit is utilized 1079.45 units were purchased. The value of the investment (price plus reinvestment of coupon) one year down the line is 112,260. The net revenue that the bank earns if this outcome materializes is 2,279.
Let us assume now that interest rates fall by 1% this impacts the reinvestment rate of coupons as well at the YTM on which the price one year later is calculated. The value of the investment one year later is now 115,617. The net revenue that the bank earns will be 5,617, i.e. an increase in the surplus of 138% over the original position.
Let us instead assume that the interest rates were to increase by 1%. Again this impacts the reinvestment rates and YTM on which the price one year later is calculated. The value of the investment one year later is now 109,231. This means there is a shortfall of 769. The surplus position has fallen 133% over the original position.
Duration matching/ immunization
We can see that the bond is very sensitive to changes in interest rates. In order to lock in the guaranteed rate of 10% over the one year period, we need to select a bond with a duration of 1. The duration of the 5-year bond given above is 3.79.
One alternative is to purchase and hold zero coupon bonds whose maturity coincides with the maturity of the liability payment date. Zero coupon bonds are price insensitive (or immune) to changes in rates as they mature at par on the maturity date regardless of how rates have fluctuated over the holding period. However, zero coupon bonds may have insufficient yield, so the bank may need to invest in coupon bearing bonds.
A coupon bearing bond with similar characteristics as the 5 year bond but with duration (Macaulay Duration) of 1 has a maturity of approximately 1 year and 1 month (maturity date of August 8, 2011). Investment in 979.03 units of this bond will yield an investment after one year of 112,363 in the original position, 112,348 when interest rates increase by 1% and 112,378 when interest rates decline by 1%. We can now see that there is very little variation (±1%) in the expected net revenue earned as compared to when we had the 5-year bond, i.e. the surplus is less sensitive to interest rate changes.
This bond satisfies one of the three conditions of immunization. Immunization is an investment strategy whereby the investment portfolio remains insensitive or immune to a general change in the rate of interest. The other two conditions are:
- The present value of assets is greater than the present value of liabilities where we calculate the present value of liabilities using the internal rate of return of the assets as the discount factor
- For this bond the IRR of assets is 12.36%. The present value of assets is 100,000 whereas the present value of liabilities is 97,897.
- The dispersion of assets must be greater than the dispersion of liabilities
- We calculate dispersion using the following formula:
The dispersion of assets (0.94) is greater than the dispersion of liabilities (0).
As we can see the bond satisfies all conditions of immunization.
ALM Applications – Pension Funds and Insurance
Portfolio dedication
The example of the zero coupon bond mentioned earlier where a number of zero coupon bonds are purchased whose aggregate par value at maturity as well as time to maturity equals the liability payment amount and date respectively, is an example of both immunization (as durations are exactly matched) as well as portfolio dedication (cash flow matching). In cash flow, matching each and every liability cash flow is matched with an equal asset cash flow. This has the advantage of eliminating interest rate risk as asset cash flows face a much smaller or no risk of reinvestment as in the case of immunization. However, as the frequency of liability payments increase it generally tends to get more costly than an immunization strategy.
The most common ALM applications of portfolio dedication are to fund the pay-out obligations of the retired lives portion of pension funds; to fund fixed payouts for insurance company products such as structured settlements.
- The first step in bond portfolio dedication is to determine the schedule of liability payments to be funded.
- Step two is to specify portfolio constraints such as sector, quality, issuer and lot sizes.
- An assumption regarding the reinvestment rate must also be made as it is not always possible to match the timing of payments and so excess funds need to be reinvested until the next liability payout date. It is desirable to have very little cash to reinvest each period as this reduces the reinvestment risk.
The benefit of a dedicated portfolio is not only a reduction in interest rate risk but could also lead to a reduction in the actuarial liability of the pension fund/ insurance product.
For example, for a pension fund, the calculation of the actuarial liability of current retired lives is dependent on an assumed actuarial investment rate. This rate is usually set conservatively because of the unpredictability of the investment performance of the fund. Conservative rates lead to increased liability which could mean higher contributions. This could diminish both corporate cash flows and current profits for the sponsoring entity.
Through a dedicated portfolio, it may be possible to fund these benefits at a higher yield than that assumed in calculating the liability. If the entity were to purchase the portfolio, the actuary could then be comfortable increasing the assumed investment rate to the yield of the dedicated portfolio. This could result in a lower actuarial liability which consequently could lead to lower current contribution requirements.

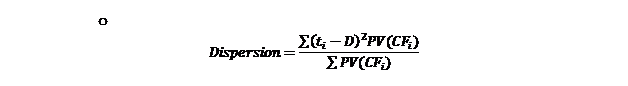
Comments are closed.