Introduction
Most end-users of options want answers to a handful of key questions about an option position: how much is the premium? Is the structure the best way to hedge a position or to take a view on a market? What are the tax, legal and regulatory implications of the trade? However, anyone trading options, anyone who has to mark option positions to market, anyone looking to close out an option position before maturity, anyone for whom the ongoing efficiency of a hedge is important, anyone who has bought a security with embedded optionality in fact just about any user of options is exposed to the complexities of option valuation. Understanding how and why the value of an option can change as the underlying changes is critical if mistakes and disappointments are to be avoided.
These complexities have led to a proliferation of different pricing models. Some of these have been designed for a particular type of option foreign exchange options, or American-style options for example. Some are responses to the known weaknesses of other models. And many were created to incorporate more sophisticated assumptions about the behaviour of the price of the underlying assets and the volatility of that price in an attempt to reflect more accurately observed market movements.
Explaining these models is beyond the scope of this chapter. The descriptions are included to enable options users to compare the different assumptions underlying the models and to highlight the fact that the price of an option depends not just on the conditions they observe in the markets but on the ways in which option dealers choose to price them. Because so much of option pricing theory is concerned with understanding the behavior of the underlying variables, much of the terminology employed comes straight from statistics. This chapter therefore also explains the key concepts and defines the technical terms most commonly used by derivatives experts terms that may not be familiar to those outside risk management.
Analytic model:
An option pricing model which, like the Black-Scholes model and its later variants, finds an explicit solution to the problem of pricing a particular option or options using mathematical functions. Black-Scholes and others, for example, specify and solve a stochastic differential equation. While these models are simple, they cannot handle the early exercise feature of American-style options. This is because the decision to exercise before expiration depends on the behaviour of the price of the underlying security throughout the life of the option and cannot be reduced to a single parameter. They are also increasingly inaccurate as the term of the option lengthens because they cannot easily take into account variations in short-term interest rates or the time-dependence of volatility. The analytical solutions on which these models are based are also known as closed-form solutions and so the models are known as closed-form [option pricing] models.
Analytic approximation models:
One of the three main classes of option pricing model (along with analytic and numerical models). Analytic approximation models may be used when traditional analytic approaches do not bear fruit. They involve a combination of theoretical analysis and simplifications judiciously chosen to make the solution tractable. One example is provided by the Barone-Adesi-Whaley model for pricing American options. Here the premium for early exercise is estimated and then added to the price of a European option which may be obtained analytically.
Antithetic variables:
This is a technique used in Monte Carlo valuation for reducing the variance of the estimate of derivative security. In its simplest form it involves creating two paths from the same set of random numbers. These paths would be mirror images of each other. The value of the derivative is calculated for each of these paths. The average of these two values has lower variance than the individual values themselves and is hence a better estimator of the value of the derivative.
Arch:
Acronym for autoregressive conditional heteroscedasticity, an econometric technique developed by Robert Engle in 1982 to model economic variables. It is an estimation procedure developed on the basis of a model of economic variables that allows the covariance matrix of these variables to change with time. It assumes that variance is stochastic and is a function of the variance of the previous time period and the absolute level of the underlying variable. Specifically, the conditional variance of a time series is allowed to depend on lagged squared residuals in an autoregressive manner. This means that during periods in which there are large unexpected shocks to the variable, its estimated variance will increase, and during periods of relative stability, its estimated variance will decrease.
Arch has found much favour in the options world as the basis for models which do not assume that volatility is constant. Most of the older option pricing models do despite the evidence to the contrary.
Instead, Arch-based models assume that volatility follows clear patterns; that today’s depends on yesterday’s and so historical volatility contains information that can be used to estimate future volatility; and in particular that volatility should regress back to its long-term average. Several other variations exists, including Garch, AGarch, EGarch and QGarch. See Garch.
Arbitrage-free model:
Option pricing models that do not allow arbitrage of the underlying variable. Most commonly applied to models developed by Cox-Ingersoll-Ross, Ho-Lee, Heath-Jarrow-Morton and Hull-White. These were originally developed to price interest rate options and incorporate constraints on the movement of interest rates designed to avoid arbitrage possibilities caused by yield curve movements. They differ essentially only in their assumptions about spot rate movements.
Autocorrelation:
The correlation between changes in a single variable over non-overlapping time periods. If a price or rate were negatively autocorrelated a move down in one period would suggest a move up the next (and vice versa). If it were positively autocorrelated then a move down would suggest a following move down (and vice versa).
Backward Induction:
This is a mathematical technique fundamental to the valuation of derivatives by tree or finite difference methods. It assumes that when making a decision an agent will maximize value based on the future expectation of returns accruing from each alternative. As an illustration of the basic principle consider the holder of an American option. At each point in time the holder will exercise the option if the value of the payoff he receives on exercise is greater than the discounted expected values of future payoffs if he does not exercise. (That is, the value of the payoff on exercise is greater than the value of the American-style option).
Barone-Adesi-Whaley:
An analytic approximation option pricing model devised in 1987 by Giovanni Barone-Adesi and Robert Whaley which incorporates a quadratic approximation approach in a very accurate model for haluing American-style calls and puts on assets which pay continuous dividends.
Binomial distribution:
The most important discrete probability distribution in options pricing. (Discrete probability distributions are those in which the underlying variable can only have certain discrete values. Most option pricing models assume continuous probability distributions such as lognormal and normal distributions.) To satisfy a binomial distribution a discrete random variable must satisfy four conditions: only two possible values can be taken on by the variable in a given time period (known as a binomial trial); for each of a succession of trials the probability of each of the two outcomes must be the same; each trial is identical; each trial is independent.
Binomial option pricing model:
An option pricing model which uses binomial trees to model the price of the underlying. This is the most common type of numerical model. The key to the binomial or binomial lattice-based model is the binomial trial process.
This divides the time until option maturity into discrete intervals or steps and presumes that during each of these intervals the key parameter typically the price or yield of a security follows a binomial process moving from its initial value S, either up to value Su with probability p or down to value Sd with probability 1 minus p. Representations of the resulting distribution resemble trees or lattices and so the series of values generated by the binomial trial process is known as a binomial tree. (More complex versions exists: a trinomial tree would allow three possible movements, and a multinomial model more than that).
The binomial process is usually specified as being path-independent that is, a move up followed by a move down results in the same price as a move down followed by a move up so that the branches recombine. Trees that do not incorporate this feature are said to be non-recombining, bushy or exploding. They are much more computationally demanding. By working backward through the lattice from expiration, at which time the value of the option is known, options can be evaluated by backward induction to discount the terminal payoff through the tree: the value of the option is that which avoids an arbitrage profit. The advantage of binomial models is that they can deal with a range of different assets, options or market conditions. So, a lattice-based model gives rise to an algorithm rather than a closed formula for determining the option value. Such models are particularly useful for valuing American-style options. The best-known is the Cox-Ross-Rubinstein model. See backward induction, Cox-Ross-Rubinstein.
Black’s Model:
This, like Garman-Kohlhagen’s model for foreign exchange, is a derivative of the original Black-Scholes model. Originally this was a model for the pricing of options on futures but it has been extended in scope to include any situation in which it is necessary to value a European option on a variable which can be assumed to be lognormally distributed about a forward price and where interest rates are non-stochastic. In particular it is frequently used to price interest rate caps and swaptions.
Black-Derman-Toy:
A single-factor (in this case short-term interest rates) term structure option pricing model proposed by Fisher Black, Emanuel Derman and William Toy in 1990 which expanded on the
Ho-Lee model by specifying a time-varying structure for volatility and incorporating it into a binomial tree of possible forward short rates.
Black-Karasinski:
A single-factor model of the term-structure where the logarithm of the short-term interest rate is assumed to be a ‘mean-reverting’ process with time-varying coefficients.
Black-Scholes:
Developed by Fischer Black and Myron Scholes in 1973, this is the classic modern option pricing model and the first general equilibrium solution for the valuation of options. The model provides a no-arbitrage value for European-style call options on shares as a function of the forward price, the exercise price of the option, the risk-free interest rate and the variance of the stock price which is assumed to follow a lognormal distribution. It does this by recognising that stocks and calls on them can be combined to construct a risk-free portfolio and that options on equities can therefore be valued using a dynamic hedging argument. That is, the option writer can exactly offset his exposure to the underlying stock by continuously buying or selling it. The model shows that, by combining the underlying stock and a money market instrument, a riskless hedge (the delta hedge) can always be formed that exactly replicates the payoff of the option to be hedged. This means that a portfolio formed by the combination of the option and its riskless hedge must appreciate at the risk-free interest rate. This riskless hedge method circumvents the difficulties of specifying investors’ risk preference and allows the risk-free interest rate to be used in the valuation process rather than some other discount rate that reflects the appropriate risk level. For any time period, the value of such a portfolio can be computed as its value at the end of the period discounted back one period at the risk-free rate. Because the price of an option is a deterministic function of the price of the underlying asset at that time, given that the distribution of asset prices is known for each time period (and in this model it is assumed to be lognormal), then the initial value of the option can be deduced by working backwards in time. For a European call option, the Black-Scholes pricing formula is:
C = SN(d1) – Ee-rT (N(d2) where d1 = ln (s/e) + (r + 0.5s2)T sT d2 = d1 – sT, N(d1) and N(d2) are the cumulative probability for a unit normal variable z That is it is the probability N(d1) = ¥òd1 f(z)dz where f(z) is distributed normally with mean zero and standard deviation of one. 1n is the natural logarithm e is the exponential T is time to maturity s2 is the instantaneous variance of the stock price which is the measure of volatility of the stock.
The equation states that the value of the call is equal to the stock price, S, minus the discounted value of the exercise price, Ee-rT, each weighted by a probability. The stock price is weighted by N(d1) which is also the hedge ratio. For each call written, the riskless hedge portfolio contains N(d1) shares of stock. On the other hand, the discounted value of the exercise price is weighted by N(d2) which is the probability that the option will finish in the money. The value of a European put, P, can be derived in a similar way as: P = Ee-rT N(-d2) – SN(-d1). The model’s great achievement is completeness: it provides a method for hedging options with the underlying asset, which allows for arbitrage pricing and hedging. Its drawbacks are that it assumes no dividends, no taxes or transaction costs, constant short-term interest rates, no penalties for short sales, that volatility and interest rates are constant, that the market operates continuously and that stock price distribution is lognormal. The generalizations of Black-Scholes address these problems, while extensions to it apply it in a modified form to options on futures (Black’s Model), options on currencies (Garman and Kohlhagen’s Model) and to exotic options.
The basic model has problems pricing short-dated options because volatility is not time-homogeneous and long-dated options because it fails to take into account mean reversion. It systematically undervalues near-maturity options, deeply out-of-the-money options, options on low volatility stocks. It systematically overvalues long-dated options, deeply in-the-money options and options on high volatility stocks. All these problems are due to the model’s assumption of the uniformity of variance across time. Other types of models address these problems.
Brownian bridge:
A Brownian Bridge defined between two points in time t0 and t1 is an arithmetic Brownian motion conditioned to take specific values x0 and x1 at those points. The distributional properties of the Brownian Bridge may sometimes be used in option pricing when time is approximated as being discrete (e.g. in binomial trees or Monte Carlo techniques) to smooth out the effect of the discretization.
Brownian motion:
Archetypal random motion. Variants of this are used as the assumed path of securities prices in many financial models.
CEV- model:
The CEV, or constant elasticity of variance, model was original proposed by Cox and Ross in 1976 to try to account for some empirical observations about equity price volatility. The specification of volatility is given as sS–a so for a=0 we have the classical model of stock prices used within Black-Scholes. With values of a greater than 0 the equity prices have high volatility when the equity price is low and low volatility when the equity price is high.
Confidence interval:
A range of values in which, with some specified probability, the value taken by a variable will lie.
Continuous variable: A variable such as time that can be subdivided into an infinite number of sub-units for measurement. The unit of measurement can therefore be increased or decreased infinitesimally. See discrete variable.
Continuous probability distribution: A distribution where the variable can take any value within a specified range such as the gain or loss from a position in a financial asset over a specified interval of time. Continuous probability distributions do not consider the probability of the variable taking on a specific value. See discrete probability distribution.
Control variates:
This is a technique available to all numerical valuation techniques. It consists of using the same technique to value not just the option whose value is required but also an option, the control, whose characteristics are close to the original option but whose value can be calculated in some more accurate manner (preferably analytically). The difference between the control’s values calculated analytically and numerically is an estimate of the error inherent in the numerical approach and is added on to the numerically calculated value of the original option. Choosing an appropriate control can result in a greatly reduced variance of the estimate.
Convexity adjustment:
The most common use of this term is to describe the adjustment that has to be made to the interest rate implied by the price of a Euro-deposit future to obtain the corresponding forward interest rate. It has come to mean any adjustment to a price obtained under simplifying assumptions to account for real-world non-linearities, for example adjusting the price of a barrier option to take account of non-uniform volatility over different deltas.
Correlation:
A measure of the degree to which changes in two variables are related. The standard measure of correlation is the correlation coefficient, a number between minus one and plus one that indicates the strength and direction of a linear relationship between two variables. A correlation coefficient of minus one indicates that they are perfectly negatively correlated, zero that they are not correlated at all and one that they are perfectly correlated.
Correlation risk is the risk that two variables or instruments are unfavourably correlated. Identifying and quantifying correlation risk has become a key element in pricing and hedging certain derivative instruments. In some options such as spread options and cross-currency caps, the correlation between the underlying assets is a first-order effect as it directly affects the option price. In quanto products, such as differential swaps, there is a second order or indirect effect, in that case between interest rates and exchange rates. See second-order effect.
Covariance:
A measure of how two random variables behave in relation to each other. Matrices of covariances are used in several different financial models, the most famous of which is Sharpe’s Capital Asset Pricing Model. It differs from correlation in that it incorporates measurements of the magnitude of the variations as opposed to the correlation coefficient which is dimensionless. The correlation coefficient between two random variables is equal to the covariance between them divided by the product of their standard deviations.
Cox-Ingersoll-Ross:
A generalization of the Black-Scholes option pricing model incorporating the work of John Cox, Stephen Ross and Jonathan Ingersoll. The model represents one of the two approaches followed by term structure option pricing models. It models the expected returns from movements in the term structure in order to price them. The second approach, followed by Ho-Lee, Heath-Jarrow-Morton, Black-Derman-Toy, and Hull-White utilizes the volatilities of the various sectors of the term structure to derive a probability distribution for an arbitrage-free binomial, trinomial or multinomial lattice of the term struc?ure.
These models all have one thing in common:
they allow for the whole-term structure to be stochastic instead of the price of a single underlying instrument or a single interest rate. The whole-term structure is represented at each node of the lattice. This methodology allows both long-term and short-term interest rate instruments to be priced with an internal consistency not possible if different models are used to price different instruments.
Cox-Ross-Rubinstein model:
The classical binomial option pricing approach first proposed by Cox, Ross and Rubinstein in 1979. It requires that u (the up-jump multiplier) is 1/d (the down-jump multiplier).
Crank-Nicholson technique:
Technique for the numerical solution of partial differential equations, which is particularly useful for diffusion equations. Since the equation satisfied by option prices is a diffusion equation it is frequently used in pricing by finite differences.
Discrete probability distribution:
A distribution of the probabilities that a variable takes certain discrete values.
Discrete variable:
A variable that can only take certain discrete values – such as whole numbers.
Differential equation:
Equation where the values of variables are implicitly related to each other through their derivatives (or rates of change). The analysis performed by Black and Scholes resulted in a differential equation where the derivatives of the value of an option with respect to time and the spot price of the underlying are related together.
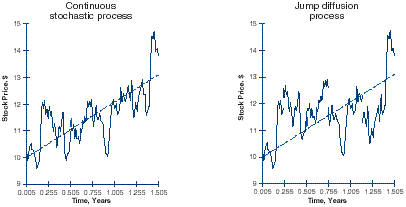
Diffusion process:
A continuous-time model of the behaviour of a random variable that uses geometric Brownian motion as its basic assumption. In the Black-Scholes model, the price of the underlying follows a pure diffusion process – that is, it is assumed to move continuously from one point to another. The consequence of this assumption is that the terminal distribution of share prices is lognormal. Other models, particularly discrete-time models, use modifications of the process.
Equilibrium model:
An equilibrium model of the yield curve makes assumptions about economic variables and economic behaviour and uses the requirement of equilibrium of the economic system to deduce the process followed by the yield curve. From this process the processes followed by discount bonds and options can be deduced. A fundamental obstacle to using this approach for pricing interest rate derivatives is that there is no guarantee that the initial term structure will be matched.
Fauré sequence:
A particular type of quasi-random number sequence. See Halton sequence.
Finite difference methodology:
An option pricing approach based on finding a numerical solution to the differential equation that the option valuation must satisfy. It does this by converting the differential equation into a series of difference equations which are then solved iteratively.
Garch:
Acronym for generalized autoregressive conditional heteroscedasticity. A variation of the pure Arch that generalizes the univariate Arch models into allowing the whole covariance matrix to change with time instead of just the variance. Several other variations exist. See Arch.
Garman-Kohlhagen:
The classic and commonly used extension of the Black-Scholes option pricing model to pricing currency options. Mark Garman and Steven Kohlhagen showed that much the same arguments apply to pricing currency options as apply to pricing stock options with adaptations to allow for the two interest rates and the fact that a currency can trade at a premium or discount forward depending on the interest rate differential. (The dividend yield is replaced by the foreign interest rate).
Gaussian distribution:
See normal distribution.
Geometric Brownian motion:
Describes the movements in a variable or asset price when the proportional change in its value in a short period of time is normally distributed. The proportional changes in two non-overlapping periods of time are uncorrelated, hence the alternative name for the process random walk. The term geometric refers to the fact that it is the proportional change in the asset price (not the absolute level) that is normally distributed. This means that the future value of a variable following geometric Brownian motion has a lognormal probability distribution and is always positive, unlike a variable following a Wiener process, whose value can become negative. This makes it mathematically useful and consequently it is the most common assumption for the movement of stock prices, stock indices, currencies and futures contracts. It is the assumption made for stock prices in the original Black-Scholes options pricing model.
Geske-Johnsonng
The Roll-Geske-Whaley model values call options on dividend-paying assets but is not applicable to American-style puts on such assets. Indeed there is no analytical solution. The Geske-Johnson model, an extension of the Roll-Geske-Whaley model, notes that there is a positive probability of early exercise of in-the-money puts which means that an American-style option can be viewed as an infinite sequence of options to exercise a European-style option. However, when the put is on an asset that pays dividends, the valuation procedure is simplified because it will not be optimal to exercise prematurely the option at any time near to but prior to an ex-dividend date. Because of its complexity, it uses trivariate normal density functions. Many market practitioners use binomial models instead.
Halton Sequence:
A particular type of quasi-random number sequence. See Fauré sequence.
<STRONG
Heath-Jarrow-Morton:
A multi-factor term structure option pricing model that uses all the information in the term structure and can handle multiple causes of term structure movement. This means that the returns on zero-coupon bonds of differing maturities are not assumed to be perfectly correlated (as is assumed, for example, by the Ho-Lee model). The most common form is a two-factor version, where the two factors are an underlying (in this case the entire term structure which is an input into the model in the same way that the current stock price is an input into Black-Scholes) and volatility – that is, a description of how the term structure fluctuates over time. This means that the model does not have to assume that all bond prices (in fact the model uses stochastic forward rates not zero coupon yields) are perfectly correlated. Instead, it assumes a random term structure of interest rates and is designed to be automatically consistent with both the observed term structure and the volatility functions input by the user. As a result of using a multi-factor model of the term structure, the model employs a multinomial instead of binomial model of term structure movement. The key difference between it and the spot rate models of Black-Derman-Toy, Vasicek, Hull-White and Cox-Ingersoll-Ross is that these models treat the spot interest rate as the underlying variable. Besides the current spot rate, these models include various parameters used to describe the possible future paths of the spot rate. Since the current term structure is not a direct input, these models try to fit the term structure by searching for parameter values which cause calculated zero coupon bond prices to match the market.
Heteroscedastic:
In simple linear regression, an error term compensates for the fact that in modelling the relationship between two variables, one of which is assumed to be the major factor in the movements of the other, movements in one will in fact be imperfectly described by movements in the other because of factors not captured by the regression model. This error term is normally distributed with a mean of zero so that its effects cancel each other out. If the variance of the error terms is constant, the regression is said to be homoscedastic. If it is not, it is said to be heteroscedastic.
Ho-Lee:
The first whole-term structure option pricing model, proposed by Thomas Ho and Sang-Bin Lee in 1986. Using a discrete-time binomial approach this single-factor model incorporates the whole term structure rather than just changes in a long or short interest rate. Given the term structure as known today, in the next time period the whole term structure can move up or down. However, the model makes a number of assumptions not borne out by empirical observations: it assumes that the returns of zero coupon bonds of different maturities (which it uses to represent the term structure at each node on the binomial lattice) move in a perfectly correlated manner and it requires that all interest rates both spot and forward have the same volatility. It also allows for negative interest rates as it does not incorporate mean reversion. Unlike Black-Scholes-type models, Ho-Lee establishes no explicit link between hedging and pricing.
Hull-White:
A single factor model developed using a trinomial lattice. It is a yield-curve based model in the same mould as the Ho-Lee, Vasicek, Heath-Jarrow-Morton and Black-Derman-Toy models. A key feature of Hull-White is that it treats mean reversion as time-dependent.
Implied correlation:
The correlation coefficient implied by the price of a two-factor option on the assumption that volatilities for the two assets involved are available. This concept is most relevant in the foreign exchange markets where there are liquid markets in, for instance, dollar-mark, dollar-yen and mark-yen options. The option prices quoted on these options give implied volatilities, the exchange rates and implied correlations between them.
Ito Process:
A generalized Wiener process where the drift and dispersion parameters are a function of state and time.
Ito’s Lemma:
An equation giving the process followed by a function of an Ito process. This is also an Ito process whose coefficients are given in terms of the derivatives of the original process with respect to state and time. This lemma (proposition) is fundamental to Black-Scholes since an option price is a function of an underlying spot price whose behaviour is conventionally assumed to be an Ito process. Knowledge of the relationship between the dispersion parameters of the two processes given by the lemma enables a risk-neutral portfolio to constructed and hence a risk-neutral price for the option to be derived as a solution to a partial differential equation whose form is also determined by the lemma.
Jump diffusion process:
The process proposed by Robert Merton whereby the price of the underlying neither simply jumps nor follows a pure diffusion process but moves by a combination of a jump followed by continuous diffusion. Option pricing models have been extended to incorporate these kinds of jump price dynamics with directional bias but there are still theoretical problems associated with jump diffusion models. For example, the underlying asset in a foreign exchange option is an exchange rate which can be denominated in either of two currencies. However, jump diffusion models do not give the same prices when compared in a common currency.
|
|
Jump process:
A stochastic process for movements in the price of the underlying proposed by John Cox and Stephen Ross. In it the price of the underlying does not follow the pure diffusion process assumed by the Black-Scholes model but rather jumps from one point to another in steps larger than traditional random processes would generate. This idea was expanded in the Cox-Ross-Rubinstein binomial model.
Kurtosis:
A measure of the extent to which probability is concentrated more around the mean and in the tails rather than in the mid-range relative to a normal distribution. A normal distribution has a kurtosis coefficient of three. Kurtosis of less than that indicates a distribution with a fat midrange on either side of the mean and a low peak – called platykurtic . A kurtosis coefficient greater than that indicates a high peak, thin midrange and fat tails – called leptokurtic. Empirically the latter is the phenomenon most frequently observed in financial prices and markets. It results in implied volatilities of vanilla options which are higher for strikes above and below the forward than for options struck at the forward – the well-known volatility smile. See volatility smile.
Least squares regression:
One of a number of types of regression analysis that measure the relationship between variables.
Linear regression:
Linear regression is a regression where the dependent variable is modelled as a linear combination of the dependent variables plus the error term. The simplest case is simple linear regression where there is only one dependent variable. Here the relationship is: y = a + bx + u, where a is a constant; b is the regression coefficient and u is the error or disturbance term.
Lognormal distribution:
A variable has a lognormal distribution if the natural logarithm of the variable is normally distributed. A consequence of the classical assumption about the process followed by assets, that it is geometric Brownian motion with drift, is that the asset price at a particular point in time in the future has a lognormal distribution. Thus when valuing an option using the risk-neutral expectation approach, to obtain for instance the classical Black-Scholes option pricing formula, we would take the expectation with respect to that lognormal distribution.
Low-Discrepancy sequences:
See quasi-random numbers.
Markov process:
A class of stochastic processes or models which define a finite set of states. The essential property of the Markov process is that the future behaviour of the process (the progression of the set of states from one state to the next) is independent of past behaviour and determinable solely from the current state. Most option pricing models assume that movements in the price of the underlying or, in the case of interest rate options, the zero-coupon curve, are determined by a Markov process.
Mean:
The sum of observation values divided by the number of observations. A statistical measure of central tendency.
Mean reversion:
The statistical tendency of variables, most relevantly stock prices, interest rates, and volatility, to trend away from extremely high or low values and to gravitate towards a long-term average level. When the value of a mean-reverting variable reaches a very high level, it is more likely to go down than to go up. When it reaches a very low level, it is more likely to go up than to go down. Mean reversion is important in option pricing because it contradicts an assumption of many early models that the variance of the price of the underlying asset of an option is directly proportional to the option’s term to expiration. This assumption implies that the statistical dispersion of asset prices will widen indefinitely further and further into the future. In interest-rate option pricing models it means that interest rates can become negative. (Interest rate models are further constrained in absolute terms: in a normal economy 100% rates are extremely unlikely.)
The practical consequence for pricing is that the longer-dated an option, the more seriously it will be mispriced by models that ignore mean reversion. To account properly for mean reversion and hence estimate the volatility of an economic variable that demonstrates it, a more complicated underlying model than geometric Brownian motion is needed. Models such as Vasicek and Cox-Ingersoll-Roll incorporate mean reversion to account for the term structure of volatility. The Hull-White model goes further by proposing that mean reversion is time-dependent.
Monte-Carlo simulation:
A generic technique involving the generation of random numbers to solve deterministic problems. It is often used by numerical option pricing models as an alternative to the binomial process as a simulation of the underlying asset price. Using computers, a Monte-Carlo simulation attempts to simulate the process that generates future movements in the price of the underlying. Each simulation results in a terminal asset value and several thousand computer simulations give a distribution of terminal asset values from which the expected asset value at option expiration can be extracted. This method is used to value complex options, particularly path-dependent options for which there is no analytical solution.
Multi-factor model:
An option pricing model in which there are two or more sources of randomness contributing to the option price. The reasons for using multi-factor models can be split into two: either the option payout itself is a function of two variables (e.g. a spread option on A or B, or an option on A that knocks out on B), or the processes of the variables appearing in the option payout are defined in terms of many factors (e.g. stochastic volatility models). See single-factor model.
Non-uniformity:
In option pricing used to refer to the fact that volatility is expected to be higher on certain days than on others.
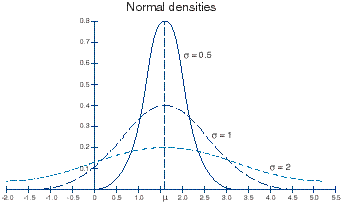
Normal distribution:
The most widely occurring frequency distribution. The normal (or Gaussian) distribution is distinguished by its symmetrical bell shape and has the statistically desirable characteristics of being completely described by the mean and standard deviation of the distribution. The mean indicates the position of the centre of the bell, the standard deviation how spread out it is. If a variable is normally distributed, 68.27% of its values will fall within plus or minus one standard deviation of the mean; 95.45% will fall within plus or minus two standard deviations and 99.73% will fall within plus or minus three standard deviations from the mean.
Numerical model:
An option pricing model which avoids the requirement to solve a stochastic differential equation by specifying a particular process for the underlying asset price and then using an iterative approach to solve the value of the option. Numerical models can be divided into three main classes: the binomial models, the finite difference models, and Monte Carlo simulations.
Poisson Process:
A process useful for describing events which happen discretely but randomly in time, e.g. crashes, central bank rate hikes. It is frequently used as a component of jump diffusion processes to describe the occurrence of the discrete jumps.
Pseudo-random numbers:
Monte Carlo techniques for valuing derivatives require a supply of random numbers which are uniformly distributed and independent. Implementation of these techniques is performed on computers which are deterministic machines and therefore not intrinsically good at creating randomness on demand. There are deterministic algorithms which generate sequences of numbers which appear to have the appropriate properties of randomness. However, because they are not truly random they are termed pseudo-random. See quasi-random numbers.
Probability density [function]:
A function associated with any distribution which specifies mathematically the way in which probability is distributed over different possible values for that distribution. So, the density function of a normal distribution is the well-known bell-shape which implies that there is a high probability of being close to the mean and low probability of being a long way from it.
Quasi-random numbers:
These sequences, like pseudo-random numbers, may be used as the random number generating process in Monte Carlo models. Successive elements of a sequence of pseudo-random numbers are designed to be independent whereas successive elements of a sequence of quasi-random numbers are not. In fact they are designed to have a certain structure which allows them to cover the probability space in as uniform a manner as possible and hence to improve the convergence of the estimation. See Fauré sequence, Halton sequence, Sobol sequence.
Rendleman and Bartter:
This is a single-factor model of the yield curve where the short rate is defined to follow Geometric Brownian Motion with drift. It is not in common use since it does not incorporate any of the mean reversion that is empirically observed.
Risk-neutral pricing principle:
Developed by John Cox and Stephen Ross, the theory that stock options may be valued as if the underlying stock’s mean rate of growth is equal to the riskless rate. In particular, the value of a European option is the discounted present value of the payoff under the risk-adjusted probability distribution for the stock price at expiry.
Roll-Geske-Whaley:
An extension to the Black-Scholes model incorporating the independent work of Richard Roll (1977), Robert Geske (1979) and Robert Whaley (1981) and providing a solution for the pricing of American-style call options on assets paying dividends. Behind the model is the observation that an American-option can be viewed as a portfolio of three options: a European option on the underlying; a European option to exercise the first option which will not be exercised until the instant before the ex-dividend date; and a compound option written on the first option (to incorporate the cost incurred by exercising the first two options of forfeiting the remaining life of the first option). The model can also be used to value calls on stock indices and American puts on stocks that do not pay dividends but cannot be used to value American puts on assets that pay dividends.
Second order effect:
Error term which occurs due to non-linear effects in a model which has been approximated by a simpler linear model. Option gamma is a second order effect. See correlation risk.
Single-factor model:
An option pricing model that incorporates only one uncertain parameter, the future price of the underlying. Such models make fixed assumptions about other variables such as the term structure of interest rates and volatility. Multi-factor models which can accept more than one parameter are better able to model interest rates and volatility and are necessary to price options on a number of underlying assets (such as spread assets) correctly. See multi-factor model.
Skew:
In statistics skew is the asymmetry of a distribution around its mean. Positive skew is an asymmetric tail extending toward positive values (right-hand side). Negative skew is an asymmetry toward negative values (left-hand side). In options skew is commonly used to refer to the volatility skew. See volatility skew.
Sobol sequences:
A particular type of quasi-random number sequence.
Stochastic volatility model:
A multi-factor model where the volatility of the process followed by the underlying is itself a stochastic, usually mean-reverting, process.
Tail:
The end (left or right hand section) of a probability distribution. Also used by futures traders either for the change in the number of futures contracts needed to hedge a position because of variation margin flows or for the number of excess futures contracts in a basis trade. Also used in the bond or note markets of a security with only a short time to maturity.
Tri-nominal tree:
An extension of the binomial method of option pricing in which the variable being modelled (the price of the underlying) is allowed three possible outcomes instead of just two: move up, move down or stay the same. This provides greater flexibility and is useful in pricing more complex products.
Variance:
The statistical measure of how widely a variable is dispersed around the mean. Standard deviation is the square root of the variance.
Volatility smile:
Refers to the influence of the out-of-moneyness of an option of a given maturity on its quoted implied volatility. Generally the implied volatility of out-of-the-money options (that is options with low deltas) is greater than that of at-the-money options. If the implied volatilities are plotted (Y-axis) versus the strike (X-axis), a curved line resembling a smile is obtained. This is due to option sellers needing a premium for selling low delta (disaster insurance) options.
This phenomenon is not consistent with the basic Black-Scholes model which implies that asset volatility is constant. If true, the implied volatility from European options of all strikes and maturities would be identical. In fact, implied Black-Scholes’ volatilities depend on the maturity and strike of the European option in question. That is, the market may believe that extreme upward and downward movements are more likely than allowed by the Black-Scholes model. In this case it is said that the implied market distribution is more leptokurtotic than that implied by Black-Scholes. This can be seen when the implied volatility smile is convex in the strike price. See kurtosis.
Volatility trading:
Taking options positions that will profit not from moves in the price of the underlying but from changes in implied volatility. Traders can take views on absolute levels of implied volatility by buying and selling combinations of options – classically delta-hedged straddles and strangles. They can also trade future actual or realized volatility versus present implied volatility, profiting if future actual volatility is more or less than the implied volatility of the position when the trade is put on. So if they believe that the volatility implied by an option is too low, then the option is cheap and they will buy it. Buyers {sellers} of realized volatility against implied volatility profit when the underlying is more {less} volatile than the implied volatility predicted. These trades are non-directional, that is they are hedged against absolute price moves in the underlying. Traders can also trade between the different implied volatilities of options at different maturities or with different strikes (smile or skew trading).
Whole-term structure pricing model:
An interest rate option pricing model that takes into account the relationships between spot rates at different points in the curve. By using the information contained in the current term structure of interest rates and also the volatilities of each of the spot rates as inputs into binomial, trinomial or multinomial trees which value the underlying debt instrument at each node, the models provide the basis for a valuation of an option on that instrument. The Ho-Lee and Heath-Jarrow-Morton models are of this type. Such models are designed to enable the exposure on all interest-rate derivative products to be aggregated. For example, the volatility exposure created by a long position in swaptions should be able to be offset by a short position in caps so that only the net volatility is hedged.
Wiener process:
The description of movements in a variable when the change in its value in a short period of time is normally distributed and the changes in two non-overlapping periods of time are uncorrelated. Also known as arithmetic Brownian motion.
Thomas A. Fetherston at the University of Albama put this together at some point in time – a mix of teaching notes, core concepts, a glossary and a 109 page handy desk reference that you would end up referring to if you work with derivatives in any shape and form.
I stumbled across this resource about 5 years ago and it had been stewing invisibly in one of the many resource folders I have on my hard drive. I believe it would be a crime to sit or hide on a resource like this. The Glossary is here and I will try and post the teaching notes over the next few days after turning them into bite sized pieces as and when I get time.
I looked for Tom’s home page but a Google search on Tom’s name only pulls up his authored books, no home page that I could possibly link to.


Comments are closed.