Earlier we had defined the input and output cells for the Black-Derman-Toy (BDT) interest rate model. In this post, we will consider how the first set of calculation cells, i.e. the short rate binomial tree will be defined in EXCEL.
It is important to note here that in constructing the interest rate model these steps just set the stage and are not necessarily the final result. That is to say in this section we simply define the formulas and necessary constructions. The outputs from these constructions are only valid after all parts of the model have been built, effectively linked and the solver function run.
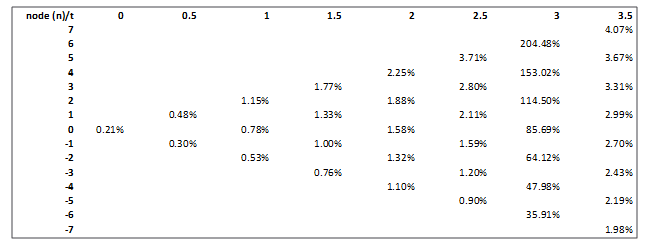
The procedure for generating the complete binomial interest rate tree is illustrated below for early durations and may be easily extended to construct the full set of short rates. These rates are calculated by using the up movements, ut and the median rates rt:
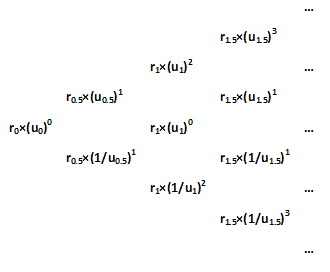
For example r0.5×(u0.5)1 = 0.38%×(1.2808)1=0.48%. As can be seen above the resulting interest rate tree is recombining.
In this post, we saw how the binomial tree of short rates of interest was calculated from the median rates and the up-movements, i.e. the output cells of the BDT model. The next post will deal with how the calculation cells for the state price lattices will be defined.

Comments are closed.