Value at Risk Limits
The company would need to decide on the level of VaR based on the risk appetite of the company.
|
They would also need to decide on how much liquidity would need to be incorporated into the VaR measure that is the time that would generally be taken to liquidate the portfolio/ sub portfolio.We recommend 1:3 VAR i.e. VaR calculated at a confidence level of 75b.% for a 10 day holding period as this represents a fairly high likelihood of loss event. In other words there is a possibility that losses will exceed the maximum loss amount one day in four days, i.e. the 1:3 odds. This will be subject to an upper bound equal to the capital loss amount specified earlier. Alternatively an appropriate level of odds may be set such that the VaR%* book size is approximately equal to the capital loss amount. | ||||||||||||||
| Figure 6: Odds, Confidence Levels & Limits |
For example if the VaR limit works out to 15.5% for the entire portfolio then the limit will be the minimum of the upper bound and the VaR amount, i.e. min (15.5%×500,000,000 , 50,000,000)= AED 50 million.
Once they decide on the level of confidence and the liquidity factor to use, the VaR limit will be determined for the entire portfolio and then for the sub-portfolios within that portfolio. This may be done as follows:
For the portfolio as a whole the limits could be set by starting with the total capital available to the trading operation and relating that to the maximum amount of VaR that can be supported by that capital, i.e. Available capital = y*10-day holding VaR. In other words the VaR limit for the total portfolio =Available capital / y*(sqrt(10)) where y is a multiple of the 10 day holding VaR. An industry standard for required capital for market risk is 3 * VAR (99% confidence level, 10-day holding),i.e. y =3.
For sub portfolios VaR will be determined as follows:
Method 1: VaR limits specify the maximum amount of VaR that each desk can cause. The practical starting point for setting VaR limits is to measure the current stand alone VaR for each desk and set the VaR limits to be a little higher or lower depending on whether the management wants the given desk to grow or shrink. This method does not account for correlations between portfolios and does not consider the overall VaR limit.
Method 2: VaR limits for the sub portfolio are defined by using the VaR limit defined for the total portfolio and then accounting for average correlations between sub portfolios. The optimal amount to be allocated to each portfolio depends on the expected revenue per unit of standalone VaR. This is illustrated in the numerical example below assuming the portfolio comprises of two sub portfolios and amounts are in millions.
Using the quadratic equation we get,
| y= | 3 |
| Available capital= | AED 1,000.00 |
| Liquidity factor= | Sqrt (10) = 3.16227766 |
| VaR Limit (total)= | AED 105.41 |
| VaR Limit % of Available capital= | 10.54% |
| Sub Portfolio | Revenue per unit of standalone VaR |
| 1 | 1.5 |
| 2 | 1.3 |
| Average Correlation of the two portfolios= | 0.3 |
| VaR Limit 1 | VaR Limit 2 | Revenue 1 | Revenue 2 | Total |
| 105 | – | 157.50 | – | 157.50 |
| 100 | 14 | 150.00 | 18.04 | 168.04 |
| 95 | 25 | 142.50 | 31.89 | 174.39 |
| 90 | 33 | 135.00 | 43.48 | 178.48 |
| 85 | 41 | 127.50 | 53.57 | 181.07 |
| 80 | 48 | 120.00 | 62.55 | 182.55 |
| 75 | 54 | 112.50 | 70.66 | 183.16 |
| 70 | 60 | 105.00 | 78.04 | 183.04 |
| 65 | 65 | 97.50 | 84.81 | 182.31 |
| 60 | 70 | 90.00 | 91.04 | 181.04 |
| 55 | 74 | 82.50 | 96.79 | 179.29 |
| 50 | 79 | 75.00 | 102.10 | 177.10 |
| 45 | 82 | 67.50 | 107.02 | 174.52 |
| 40 | 86 | 60.00 | 111.57 | 171.57 |
| 35 | 89 | 52.50 | 115.77 | 168.27 |
| 30 | 92 | 45.00 | 119.63 | 164.63 |
| 25 | 95 | 37.50 | 123.18 | 160.68 |
| 20 | 97 | 30.00 | 126.43 | 156.43 |
| 15 | 100 | 22.50 | 129.38 | 151.88 |
| 10 | 102 | 15.00 | 132.04 | 147.04 |
| 5 | 103 | 7.50 | 134.41 | 141.91 |
| – | 105 | – | 136.50 | 136.50 |
Figure 7: Example – Setting VaR limits for sub portfolios
Based on the maximum revenue, the optimal VaR limits for the sub portfolios are AED 75 for sub portfolio 1 and AED 54 for sub portfolio 2.
Regulatory Limits
Under Basel 2’s IMA approach VaR is set at a 99% confidence level over a 10-day holding period. This will be subject to an upper bound equal to a multiple of the capital loss amount.
The multiple will be determined as follows:
| Multiple | Upper Bound on VaR Limit |
| Normsinv (99%)-Normsinv (75%) = 2.326-0.674 = 1.65 | 1.65 × 50000000 = 82,592,906 |
| Normsinv (99%)-Normsinv (60%) = 2.326-0.253 = 2.07 | 2.07 × 50000000 = 103,650,039 |
Figure 8: Determination of multiple for setting an upper bound on VaR limit
Normsinv (.) = inverse of the standard normal distribution.
For example if the VaR limit is based on a 75% confidence level and if the regulatory approach VaR works out to 15.5% of the entire portfolio then the limit will be the minimum of the upper bound (based on ratio) and the VaR amount, i.e. min (15.5%×500,000,000 , 82,592,906)= AED 77.5 million

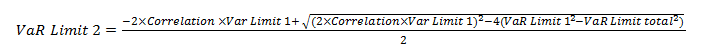
Comments are closed.