Beta is a quantitative measure of the volatility or systematic risk of a given instrument (e.g. equity) to that of the portfolio to which the instrument is a part. It is a correlation measure of the non-diversifiable risk of the instrument in relation to the market.
In the Capital Asset Pricing Model (CAPM) formulation, the portfolio is the market portfolio that contains all the risky assets. Usually for calculation purposes the market portfolio is replaced by a proxy such as a broad, well-diversified, market index.
Betas greater than 1 mean that the underlying instrument is likely to move more, i.e. with greater volatility, than the market movement. Betas less than 1 signify that the underlying instrument is likely to move less, i.e. with lower volatility, than the market movement. A beta equal to 1 indicates that the instrument is likely to move in tandem with the market.
However, instrument betas should not be viewed in isolation; meaning that a value of 0.6 for beta is not necessarily better than a figure of 1.4. These results should be assessed along with the entity’s portfolio construction strategy and view on the market. In general, a higher beta is viewed as better for a bull market where the instrument’s price is expected to rise at a fast rate than that of the market index whereas a lower beta is viewed more favorably when conditions are more bearish where the instrument’s price is expected to fall at a slow pace than that of the market.
The formula for the beta of an asset within a portfolio is given below:

Where
ra = rate of return of the asset
rp = rate of return of the portfolio of which the asset is a part
Cov(ra, rp)= Covariance between the rates of return of the asset and the portfolio
Var(rp)= Variance in the portfolio’s rates of return
As mentioned earlier in CAPM the portfolio is the market portfolio containing all risky assets. This means that in the formula above the rp terms will be replaced by rm, the rate of return of the market, alternatively proxied by the rates of return on a broad market index.
In EXCEL covariance is given by the following formula:
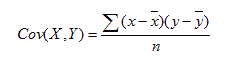
Where
x = rate of return for the asset X
x_bar = average of the rates of the return for asset X
y = rate of return for the asset Y
y_bar = average of the rates of the return for asset Y
n = sample size
and may be calculated by using the function COVAR(array for stock ABC returns, array for Broad Market Index returns).
In turn in EXCEL variance is given by the following formula:
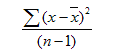
Where
x = rate of return for the asset X
x_bar = average of the rates of the return for asset X
n = sample size
and may be calculated by using the function VAR(array for Broad Market Index returns).
Let us now review the step-by-step calculation methodology for beta in EXCEL.
First obtain the time series price data over the given period of analysis for the given instruments as well as the broad market index.
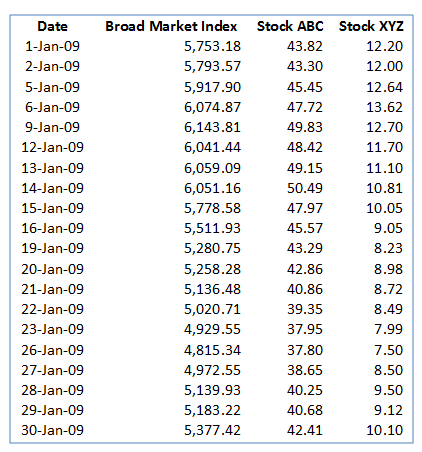
Next, calculate the daily return time series from the price data. The daily returns are calculated by taking the natural logarithm of the ratio of successive (consecutive) prices:
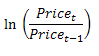
The resulting return series is given below:
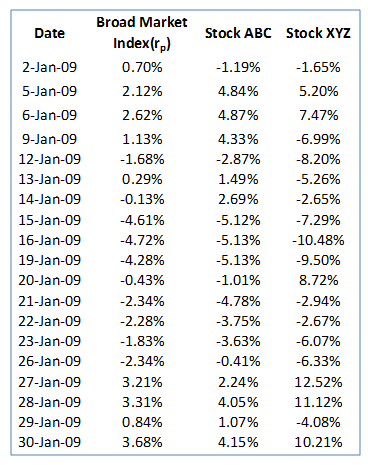
Then using EXCEL’s COVAR() function determine the covariance between the stock’s return and the broad market index returns. This is illustrated below for Stock ABC:
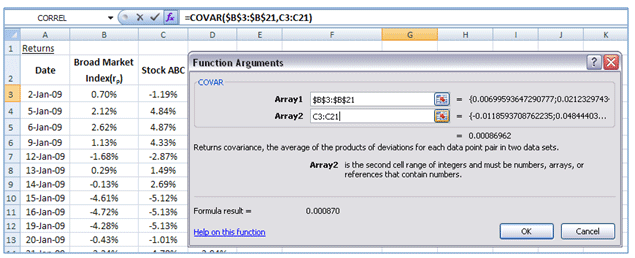
The covariance of stock ABC’s returns with the returns of broad market index works out to 0.000870.
Next, use EXCEL’s VAR() function to determine the variance in the broad market index returns. This is illustrated in the snap shot below:
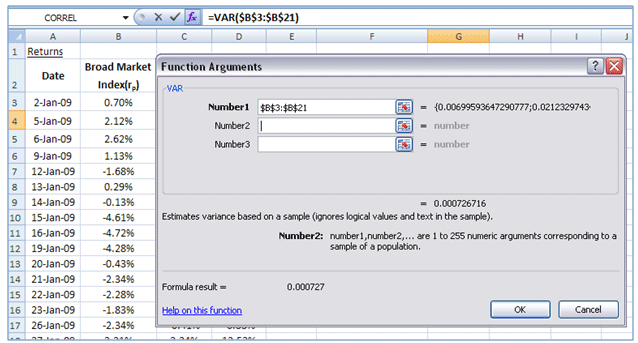
The variance in the broad market index returns works out to 0.000727.
Finally we bring these two pieces of formula together. Recall that the formula for beta is:
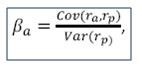
Therefore, beta for Stock ABC with respect to the Broad Market Index will be:
Covariance of the returns for Stock ABC and the Broad Market Index ÷ Variance in the Broad Market Index Returns = 0.000870/0.000727=1.20. This means that when the market moved, the prices of ABC stock moved 20% more than the market, i.e. the stock prices exhibited greater volatility than the market.
[As you may have noticed the covariance measure in EXCEL uses the sample size, n, in the denominator, whereas the variance measure uses the sample size less one, i.e. n-1, in the denominator. For the sake of consistency or to calculate the exact value of Beta using the existing EXCEL functions we need to make an adjustment to the COVAR() derived value as follows:
COVAR()×(n)/(n-1)
In our example the adjusted covariance that results is 0.000918 instead of 0.000870 whereas the beta works out to 1.26 instead of 1.20.
However for a simple indicative analysis of the systemic correlation between the instrument and the broad market index as suggested by Beta, given that the data set will be larger the EXCEL calculation of COVAR()/VAR() should suffice.]

Comments are closed.