Black Scholes, Derivative Pricing and Binomial Trees
1. Black Scholes Formula
a. Call Option price (c)
b. Put Option price (p)
Where
N(x) is the cumulative probability distribution function (pdf) for a standardized normal distribution
S0 is the price of the underlying asset at time zero
K is the strike or exercise price
r is the continuously compounded risk free rate
σ is the volatility of the asset price
T is the time to maturity of the option
q is the yield rate on the underlying asset. Alternatively, if the asset provides cash income, instead of a yield, q will be set to zero in the formula and the present value of the cash income during the life of the option will be subtracted from S0.
2. Greeks
a. Delta
b. Gamma
Where
is the standard normal density function.
c. Theta (per year)
d. Vega (per %)
e. Rho (per %)
3. Binomial Tree
a. Probability
Where p is the probability that at the end of the time step, Δt, the price (S) will move up to Su. Alternatively 1-p is the probability that the price will move down to Sd.
r is the risk free rate
q is the dividend yield
σ is the volatility of the prices
b. Price at node
 c. Payoffs at nodes (1 step tree) – European Call Option
c. Payoffs at nodes (1 step tree) – European Call Option
d. Price of a European Call option (1 step tree)
Price of the option (value at time 0) = Expected present value of payoffs = C=e-rΔt{pCu + (1-p)Cd}








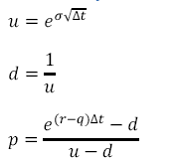
Comments are closed.