Monte Carlo Simulation revisited – Fixing the distribution
I have always wondered wondered what would happen if I could bring two simulation approaches together. Run a simulation using the Monte Carlo method, but use the true historical distribution rather than the default Normal selection simulation models pick.
The original Monte Carlo Simulation model uses the following process:
The revised hybrid approach tweaked it to the following variant.
The Hybrid Monte Carlo Simulation Model – Using the actual historical distribution
Last week we re-ran our models for three interesting commodities and one currency.
- Oil – Spot prices – WTI Bench Mark
- Gold
- Silver
- Euro-USD Exchange rate
Monte Carlo simulation and historical returns – Calculating Value at Risk (VaR)
A natural question that should come up after the above discussion is how does the hybrid Monte Carlo simulation model using historical returns fare in terms of Value at Risk measurement compared to the traditional Monte Carlo simulation (based on the normally scaled random numbers) as well as the original Historical simulation approaches?
We answer this question by estimating Value at Risk numbers obtained using each of these three methods for Gold, Silver, Crude spot prices and the EUR-USD exchange rates.
The traditional Monte Carlo simulation model (here also called the MC-Normal approach) for simulating prices and the one derived using zt‘s that are derived from historical returns (here also called the MC- Historical approach) have been discussed in our prior posts and the reader may consider reviewing these methodologies before proceeding ahead.
Calculating Value at Risk: Step by Step case study
Once the price streams have been simulated, the returns series are determined by taking the natural log of the ratio of successive prices. In our example we have projected daily prices for a 365-day period to obtain 364 daily returns. For the historical simulation approach we have used a window of 365 days of the most recent actual prices available to us.
For the MC model using historical returns we have indexed rates for the years January 2004 – December 2012. This has been done by dividing the width of the random number space (i.e. 1) into equal intervals for the total number of return observations. 8 years of data was used specifically to improve and increase the number of actual “outliers” and provide a more complete true distribution for the simulation model.
We may use EXCEL’s Data Analysis Histogram functionality to then plot a histogram of returns for each of these methods and determine the Daily VaR number from the histogram values and chart output. In our example we have actually created the histogram ourselves so that it automatically updates as scenarios change. The methodology for doing this and for calculating daily VaR from the histogram is discussed in the following post and may be applied in the same manner to all three approaches being considered here:
Comparing VaR Models, methods & metrics” (see the section on Historical Simulation VaR Approach)
The results of our analysis are given below:
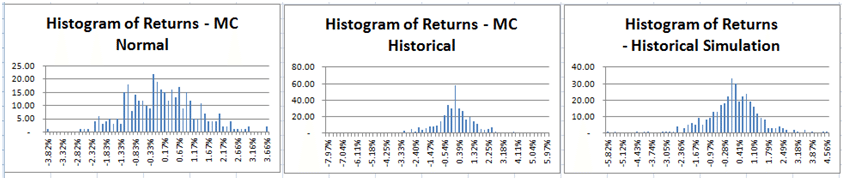
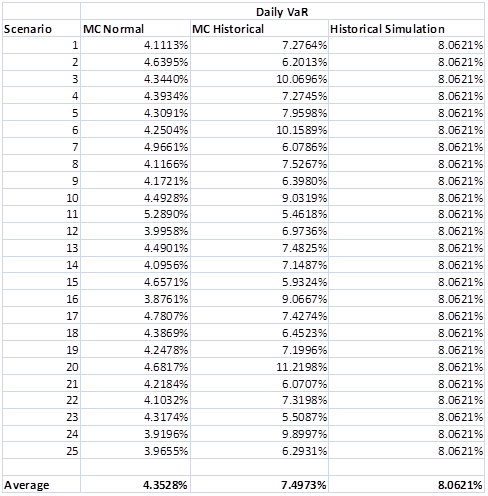
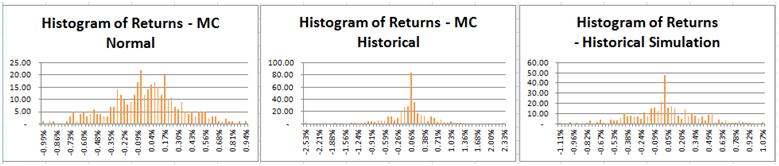
Comparing Monte Carlo Simulation Models & Methods – Gold Prices & Value at Risk Estimates.
The histogram of returns for the Monte Carlo simulation model that uses the normally scaled random numbers has a much narrower dispersion of values around the mean and does not capture the level of extreme events seen in the gold price series over the past years. Value at Risk (VaR) from the Monte Carlo simulation using the historical returns reflects these extreme events in its tails. Across the 25 scenarios shown above the daily VaR number using the MC – Historical approach is more in line with the daily VaR number obtained using the Historical simulation approach relative to the daily VaR number from the MC- Normal approach.
Note: For the Gold MC model we have assumed an initial spot price of USD 1,657.50 (as at 28-12-2012), an annualized volatility of20.90% (for 2012 daily price returns, a risk free rate of0.16% (I year US Treasury yield curve rates as at31-12-2012) convenience yield of 0%.
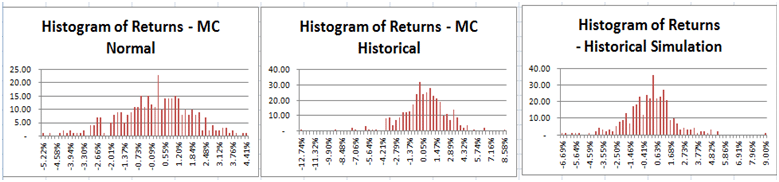
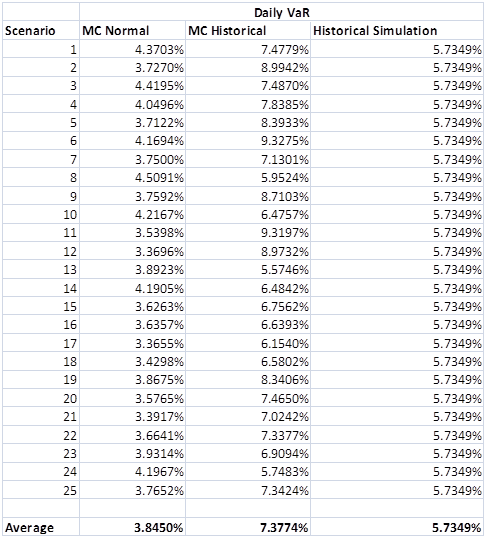
Comparing Monte Carlo Simulation Models & Methods – Silver Prices & Value at Risk Estimates.
Note: For the Silver MC model we have assumed an initial spot price of USD 30.15 ((as at 28-12-2012), an annualized volatility of of34.83% (for 2012 daily price returns, a risk free rate of0.16% (I year US Treasury yield curve rates as at31-12-2012) convenience yield of 0%.
Comparing Monte Carlo Simulation Models & Methods – Crude Oil WTI Prices & Value at Risk Estimates.
Note: For the Crude MC model we have assumed an initial spot price of USD 90.91 ((as at 27-12-2012), an annualized volatility of of31.37% (for 2012 daily price returns, a risk free rate of0.16% (I year US Treasury yield curve rates as at31-12-2012) convenience yield of 0%.
Comparing Monte Carlo Simulation Models & Methods – EUR-USD Exchange Rate & Value at Risk Estimates.
Note: For the EUR-USD MC model we have assumed an initial spot EUR-USD exchange rate of 1.3215 ((as at 31-12-2012), an annualized volatility of of6.73% (for 2012 daily price returns, a USD risk free rate of0.16% (I year US Treasury yield curve rates as at 31-12-2012) and a EUR risk free rate of 0.44% (1 year Euro Libor rate as at 31-12-2012).
In general, the VaR calculated using the MC- Historical approach is more in line with VaR derived using the Historical simulation method, sometimes producing even more conservative results. The latter happens because of the wider window used for determining indexed rates that are used to determine the uncertain component, zt, of the MC – Historical model, in relation to the 1-year window used for the Historical simulation approach.






Comments are closed.