Let’s work with the example from our previous post running the numbers using our new formulas to calculate the net present value of cashflows and an interest rate or discount rate of 10% a year.
We make one additional assumption that all payments, investments as well as returns are made at the end of the year. Since the total time period over which investments are made and returns are paid is 7 years the term of this investment is 7 years. In the discussion that follows we will simply refer to this as earning interest at a certain rate over a 7year period.
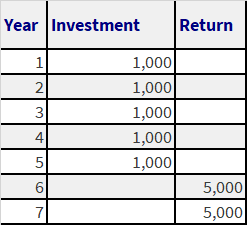
The net present value (NPV) of this opportunity, as stated earlier, is the present value of the return less the present value of the investment stream.
Present value of investment cashflows
Step One – Calculate the Discount Factors for 7 years
(1 + 10%) ^ 1 = 1.1
(1 + 10%) ^ 2 = 1.21
(1 + 10%) ^ 3 = 1.33
(1 + 10%) ^ 4 = 1.46
(1 + 10%) ^ 5 = 1.61
(1 + 10%) ^ 6 = 1.77
(1 + 10%) ^ 7 = 1.95
Step Two – Calculate the PV of investment stream
Year 1 = 1,000 / 1.1 = 909
Year 2 = 1,000 / 1.21 = 826
Year 3 = 1,000 / 1.33 = 751
Year 4 = 1,000 / 1.46 = 683
Year 5 = 1,000 / 1.61 = 621
Total PV of investment stream = PV Year 1 + PV Year 2 + PV Year 3 + PV Year 4 + PV Year 5
PV of investment stream = 909 + 826 + 751 + 683 + 621 = 3,791
Step Three – Calculate the PV of the return stream
Year 6 = 3,000 / 1.77 = 1,693
Year 7 = 3,000 / 1.95 = 1,539
Total PV of return stream = PV Year 6 + PV Year 7
PV of return stream = 1,693 + 1,539 = 3,233
Step Four – Calculate Net Present Value of cashflows
Net Present Value = PV of Return Stream – PV of Investment Stream
Net Present Value = 3,233 – 3791 = (558)
Step Five – Analyze results
Using a discount rate of 10%, the net present value of cashflows, or NPV of this investment is negative 558 dollars, which means that to earn a return of 10% you still need 558 dollars today. What are our options?
Option A
Do not invest and look for better investment opportunities.
Option B
Reduce the first year payment of 1,000 dollars by the future value of 558 dollars.
Future value of 558 dollars one year from now = 558 * (1 + 10%) = 614
This means that the instead of paying 1,000 dollars at the end of year one, we will pay 386 dollars at the end of year one and 1,000 dollars thereafter for the remaining term.
Option C
Increase return payments at the end of year 6 or year 7 or both.
We will do the six-year calculation for illustration. What we need is a number 6 years from now which will give PV of 558 dollars today. Alternatively we need the future value of 558 dollars 6 years from today.
Future value of 558 dollars six years from now = 558 * (1+10%)^6 = 558 * 1.77 = 988
This implies that we would need to get 988 dollars at the end of year 6 for us to earn 10% over a seven year period

Comments are closed.