Description: Teaches you to calculate the Internal Rate of Return or IRR.
This post follows in continuation to our previous post on calculating the Net Present Value of Cashflows. In this post we look at the rate of return that results in a NPV of zero.
Option D
Lower your expected return. We know that we can’t earn 10% per annum for seven years on this investment. What is the rate that we can earn?
There are a number of ways of answering this question:
- If you have access to MS Excel, you can set up the whole investment and run Goal Seek to find the magic number.
- If you don’t have access to MS Excel and prefer to do the whole thing by hand, we can try the manual approach ( It pays to know the basics…)
Let’s start with two points. Point A is at 10% interest. Point B is at 0% interest.
0% – 10% is the size of the interval. We lose 588 dollars at Point A (NPV = (588)). We gain 1,000 dollars at Point B (NPV = 1,000).
Step One
Reduce the interval to half its size.
Point A is still at 10%. Point B is now at 5%. If we calculate the NPV at 5% we find that it is 41 dollars
Step Two
Find the value at the two ends of the new interval. One of them should be above your target value, the other should be below your target value. Repeat Step One till you are close to your target value
Point A is still on the plus side, while point B is still on the negative side. Our target value is NPV of zero.
We again reduce the interval by half. Point B is still at 5% but Point A is now at 7.5%. The NPV at Point A is now (294)
We repeat the process again. Point A is at 7.5%. Point B is now at 6.25%. NPV is (136). We are now at a point where both ends of the interval have a negative NPV. This means that we have overshot our answer and that the solution lies between 6.25 and 5%. Now Point A is at 6.25% and Point B is at 5%.
If we repeat the process a few more times, we will find that a close approximation (NPV = .6) and 5.28% (NPV = -.3). The table below summarizes the above discussion and presents the next few steps:

Internal Rate of Return (IRR) examples and comments
The final result is that over a 7-year period, the above investment allows us to earn an interest rate of 5.27% per annum. This is also known as the Internal Rate of Return or IRR. The IRR for any investment is the rate at which the Net Present Value is equal to zero. That is, the IRR (also known as the adjusted rate of return or true rate of return) is the discount rate at which the discounted cash inflows are exactly equal to the discounted cash outflows.
Let’s do a few more examples that bring everything together from the last few posts.
Example # 1
- Invest 10,000 today
- One year from today receives 5,000
- Two years from today receives 2,500
- Three years from today receives 3,000
- Four years from today receives 3,000
What is the present value of your investment?
Solution
PV of Investment = $10,000 ( since you invest %10,000 today, and don’t do any further investments)
First we calculate the discount rates for the 4 years:
- 1st year discount factor = (1 + 10%) ^ 1 = 1.1
- 2nd year discount factor = (1 + 10%) ^ 2 = 1.21
- 3rd year discount factor = (1 + 10%) ^ 3 = 1.33
- 4th year discount factor = (1 + 10%) ^ 4 = 1.46
PV of Return = PV of $5000 (1 year from now) + PV of $ 2500 (2 years from now) + PV of $3000 (3 years from now) + PV of $ 3000 ( 4 years from now).

Therefore the NPV of your investment = 10920 – 10000 = 920
Example # 2
- Invest 10,000 today
- One year from now invest 10,000
- Two years from now invest 10,000
- Three years from now invest 10,000
- You earn a return of 10% every year
What is your balance at the end of four years?
Solution

Therefore, the amount available at the end of year 4 is $ 56,156
Example # 3 – IRR
As the CFO of her new bio-tech company, Anita has to decide whether to invest in Project MadMen. The project requires a $1000,000 initial investment followed by $100,000 for the next 2 years, and $20,000 for the 2 years after that. It guarantees a $5,000,000 return in year 6. Her company has a policy to reject any project that has an IRR of less than 25%. Should she invest in or reject this project?
Solution
The IRR is simply the discount rate which makes the NPV of the investment equal to 0.
Unless you have an application that can do this calculation for you, like MS Excel, the only way to do this is by trial and error which is done here:
[Note: NPV is calculated the same way as done in previous examples. The calculation has not be shown here for purposes of simplicity]
Investment Cash Flows

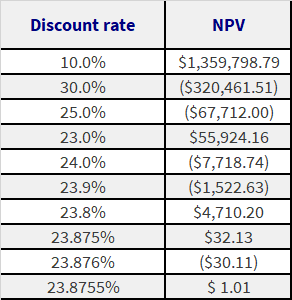
Hence the Internal Rate of Return for this project is approx. 23.8755%. Since this is below her company’s 25% requirement, Anita should reject this project.
Example # 4
In the examples above, we had ignored the issue of time value of money for the purpose of simplicity. However, it is now time to return to reality. How would your investment decision change if you had a discount rate of 10%?
We now need to find out the Net Present Value (NPV) of the two cash flows, which is simply the net profit after discounting.
Data
We know that:
Investment 1 Cash Flows:

- Minimum investment requirement = $ 100.0
- Equity = $ 50.0
- Debt = $ 50.0
Investment 2 Cash Flows:

- Minimum investment requirement = $ 50.0
- Equity = $ 50.0
- Debt = $ –
- Discount rate = 10%
Solution
The discount factor for a year can be calculated by Factor for year n = (1 + [discount rate])^n where ‘^’ stands for “to the power of”
Hence:

Dividing each cash flow with the appropriate discount factor gives us its present value:
Present value of Investment 1 Cash Flows:

PV of Investment 2 Cash Flows:

Adding up these cash flows for each investment and subtracting the initial investment gives us the NPV of the investment.
Therefore:
NPV of Investment 1 = 45 + 41 + 38 + 34 – 100 = $ 58.5
NPV of Investment 2 = 0 + 0 + 0 + 85 – 50 = $ 35.4
The NPV of Investment 1 is greater than that of Investment 2. Does that mean that Investment 1 is better? Don’t let the absolute numbers deceive you! You should look at the relative numbers, i.e. account for the capital invested. The ROIC ratio does this:
Investment 1:
- ROIC = 58.5 / 100 = 58.5%
- ROE = 58.5 / 50 = 117.0%
- Payback period = 3 years
Investment 2:
- ROIC = 35.4 / 50 = 70.8%
- ROE = 35.4 / 50 = 70.8%
- Payback period = 4 years
Again using ROIC as a measure, we can see that investment 2 is a better value that investment 1. However, we see that taking into account a discount rate has decreased the returns on the Investments.
[Note: The farther the payment from now, the bigger the impact of discounting. You can see this by comparing the discount factors for each year. In fact, a discount rate of 20% (which is high – but plausible) actually makes investment 1 (at ROIC = 29.4%) better than investment 2 (at ROIC = 20.6%)! It would be a good exercise to work this out for yourself]Example # 5 – IRR
Another means of comparing investments is through the Internal Rate of Return (IRR). Using this method, which investment would you chose?
The IRR is simply the discount rate, which makes the NPV of the investment equal to 0.Unless you have an application that can do this calculation for you, like MS Excel, the only way to do this is by trail and error which is done here:
Investment 1 Cash Flows:

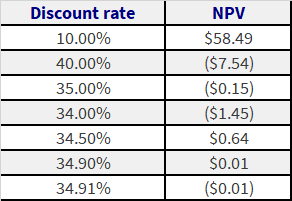
Investment 2 Cash Flows:


From the IRR calculations, we can see how these investments are on a standalone basis. For example we can see that Investment 1 has an IRR of approximately 34.9%. This means that for any discount rate below 34.9%, Investment 1 has a positive NPV. If we believe that the actual discount rate would be less than 34.9% (which is very high) then Investment 1 might be an investment we are interested in. (The final decision would take into account other investing opportunities, and the required return – to be discussed later.)
Another point of interest: Investment 1 has an IRR of about 34.9% and Investment 2 has an IRR of approximately 25.75%. It seems that Investment 1 is better that Investment 2!!
So what exactly is going on here? Well the IRR method shows you the sensitivity of the returns to the discount rate. Investment 2 just gives one payment in year 4, while Investment 1 gives a payment every year. Thus the value of Investment 2 falls a lot quicker with the increase in discount rates i.e. it is more sensitive to the discount rate.
Analyzing two investments with same capital base:
We can use internal rate of return to see which investment is better by analyzing where the IRR schedules of these two investments cross each other. One way to do this is to calculate the discount rate that makes the difference between the NPVs of the two investments equal to zero. In order to do this calculation, we need to make sure that we use the same capital base (so that we can compare the NPVs, as discussed in the example above.)
We hence recreate Investment 2 with a base of $100.
Investment 2 Cash Flows:

Investment 1 Vs Investment 2
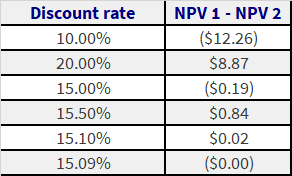
We see from above that Investment 1 and Investment 2 cross each other at around 15.09%. Thus at any discount rate below this, Investment 2 outdoes Investment 1. The situation is reversed for any discount rate above 15.09%. Hence we can see that in deciding on an investment it is essential to gauge how realistic your assumption of the discount rate is and to analyze the sensitivity of the investment’s NPV to the discount rate. In this case, if we believe that the discount rate is most likely between 8% to 12%, Investment 2 would be the investment for us.

Comments are closed.