We use the bootstrapping bonds method to derive the zero curve from the par term structure. This is an iterative process that allows us to calculate a zero coupon yield curve from the rates/ prices of coupon bearing instruments. The step by step procedure employed in given below:
Develop the Cash Flows Matrix
Given the default par term structure above we calculate the cash flows for coupon bearing instruments for each tenor. We assume that the par value for each instrument is 100. The assumption of par for the instruments means that the coupon rate is equal to the par rate. An instrument with 1 year tenor, means a cash flow at maturity of the face value, 100 plus a coupon of par rate * face value= 12.15%*100 = 12.15 or a total of 112.15. An instrument with a tenor of 2 years will have a coupon payment at the end of year 1 and a payment of the face value + coupon at the end of year 2, and so on. Further details of the cash flows are given in the matrix below:
| Coupon | 12.15% | 12.27% | 12.38% | 12.41% |
| Tenor/ Duration | 1 | 2 | 3 | 4 |
| 1 | 112.15 | 12.27 | 12.38 | 12.41 |
| 2 | 112.27 | 12.38 | 12.41 | |
| 3 | 112.38 | 12.41 | ||
| 4 | 112.41 |
The columns pertain to a particular tenor; the rows pertain to the duration when a payment is due within the tenor.
Develop the discounted value of cash flows matrix and the zero curve
As mentioned above, as the instruments are assumed to be priced at par the total present value of the future cash flows must equal the face value of the instrument, i.e. 100. In order to calculate the discounted cash flows and derive the zero coupon rates we start with the shortest tenor and work our way to the larger tenors. This is illustrated for the first two tenors below using timelines to help in understanding the bootstrapping bonds process more clearly.
Tenor 1
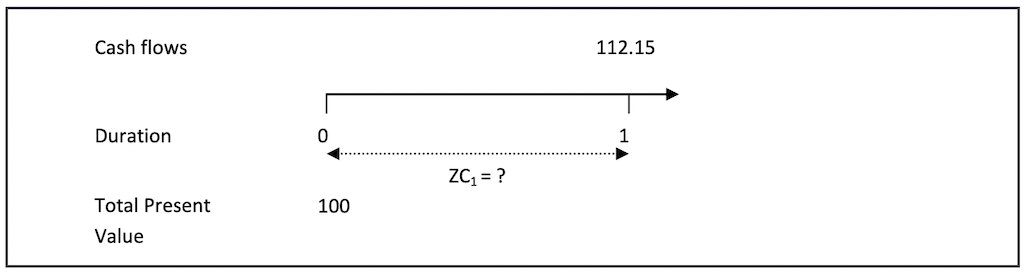
As mentioned above the total present value of cash flows is equal to the face value. For the coupon bearing instrument with tenor 1, the cash flow is due at duration 1 amounting to 112.15. We know that the discount value of this total cash flow is 100. The zero coupon rate, therefore, would be the rate that discounts the cash flows to this value, i.e.
112.15 ÷ (1+ZC1) = 100
Therefore ZC1 = [112.15 ÷ 100] -1 =12.15%
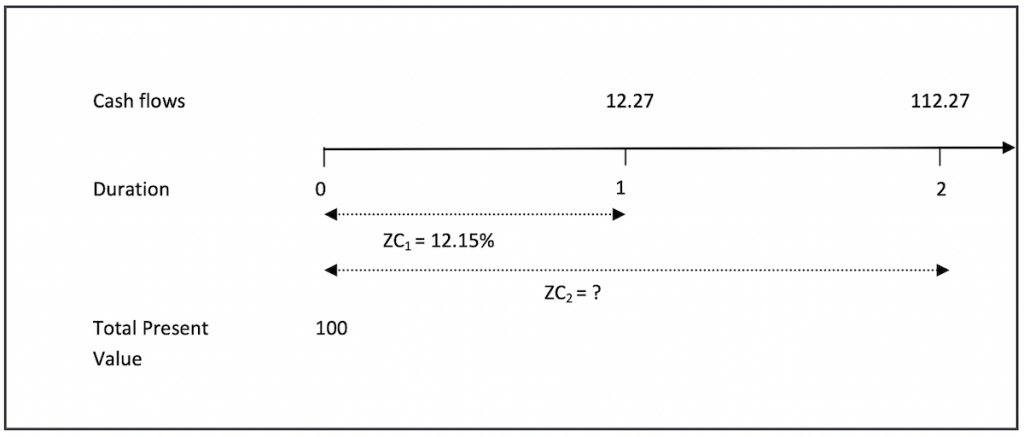
Tenor 2
The cash flow at duration 1 will be discounted using the zero coupon rate determined earlier, i.e. ZC1=12.15%. The cash flow at duration 2 will be discounted at ZC2 (annually compounded rate) which is an unknown at this point in time. Using the fact the total present value is equal to the face value, we determine ZC2 by solving the following equation:
100 = [12.27 ÷ (1+ZC1)] + [112.27 ÷ (1+ZC2)2]
(1+ZC2)2 = 112.27 ÷ {100 – [12.27 ÷ (1+12.15%)]} = 1.2606021
ZC2 = (√1.2606021)-1 =12.277%
We use the same iterative and substitution bootstrapping bonds process to derive the zero curve rates for the other tenors.
The matrix of discounted cash flows is given below:
| Tenor/ Duration | 1 | 2 | 3 | 4 |
| 1 | 100 | 10.9407 | 11.03879 | 11.06554 |
| 2 | 89.0593 | 9.820558 | 9.844356 | |
| 3 | 79.14065 | 8.739416 | ||
| 4 | 70.35069 | |||
| Total PV | 100 | 100 | 100 | 100 |
Zero Curve Term Structure
The zero curve is as follows:
| t | ZCt |
| 1 | 12.150% |
| 2 | 12.277% |
| 3 | 12.399% |
| 4 | 12.431% |
In our next post, we will learn how to calculate the forward curve from the zero rate curve just derived.


Comments are closed.