Thomas A. Fetherston at the University of Albama put this together at some point in time, possibly for his students – a mix of teaching notes, core concepts, a glossary and a 109 page handy desk reference that you would end up referring to if you work with derivatives in any shape and form.
I stumbled across this resource about 5 years ago and it had been stewing invisibly in one of the many resource folders I have on my hard drive. I believe it would be a crime to sit or hide on a resource like this. The Glossary is here and I will try and post the teaching notes over the next few days after turning them into bite sized pieces as and when I get time.
I have looked for Tom’s home page but a Google search on Tom’s name only pulls up his authored books, no home page that I could possibly link to.
Basic options terms
Key concepts
The options market, like other financial markets, has developed its own jargon. Some of this is necessary to express the basic operation of options contracts (such as ‘premium’ or ‘exercise price’) and some of it is the result of the mathematical complexity of option pricing. In particular, it is impossible for any potential user of options to avoid contact with the ‘Greeks’ a set of Greek letters used to denote variables used in option valuation.
However, although the underlying mathematics used in today’s option pricing models can be complicated and well beyond the grasp of non-mathematicians, it is not necessary to understand advanced calculus nor even the key variables such as delta and gamma respectively the first and second derivatives of the option premium with respect to the price of the underlying. For an end-user who needs to hedge an underlying cash position, or an investor who wishes to take a directional view on a market, the concepts that the ‘Greeks’ represent and their impact on the price of any particular option are intuitive and easy to grasp.
This chapter explains all the terms an end-user of options (as opposed to a professional trader) is likely to encounter in putting together an options trade. For easy reference, ‘Greeks’ are listed below with a brief explanation. For more complete details, read the individual entries overleaf.
Delta (³): The change in option value for a given change in the value of the underlying.
Gamma (G): The change in the delta of an option for a one-unit change in the price of the underlying.
Rho (R): The change in option value for a one percentage point change in interest or discount rates.
Sigma (): The standard deviation or volatility of the instrument underlying an option.
Theta (Q): The change in option value over (usually) one day keeping strike, volatility and discount rate the same.
Vega: (V) The change in option value for a small movement in volatility.
Lambda (L): The change in option value for a small change in the dividend rate (equity options) or foreign interest rate (foreign exchange options)
American-style:
An American-style option can be exercised at any point during its life. In cases where early exercise is beneficial (for example, deep in-the-money calls {puts} on underlying stocks with large {small} dividends), American-style options are more expensive than European-style options. However for options on non-dividend-paying stocks the American-style call option is the same price as the European-style. See Bermudan-style, European-style, option.
Assignment:
Notice to an option writer that an option has been exercised. In the swap market, assignment zis the transfer of a swap obligation to another counterparty.
Asymmetric payoff:
The skewed profit pattern associated with options that gives profit sharing on the upside (appreciation of the underlying for a call, depreciation for a put) while limiting liability on the downside. Contrast with the symmetrical payoff associated with forwards and futures.
At-the-money:
An option is at-the-money forward if its strike price option is equal to the current implied forward price of the underlying. A useful rule of thumb for the approximate price of an at-the-money forward option is Price = 0.4 * volatility * time * discount factor. For example, a three-month EUR Call/USD Put with a strike of 1.0370 and with a forward rate at 1.0370 and volatility of 10% would cost approximately 0.4*0.1*sqrt(0.25)*0.992 = 1.90%. The Black-Scholes price is 1.92%.
Options are often struck at-the-money forward but can also be struck at-the-money spot. This is the point at which the strike is equal to the prevailing spot price of the underlying. An interest rate cap struck at the current Libor level is at-the-money spot; one struck at the current swap rate for the period of the cap (or the FRA rate for a caplet) is at-the-money forward.
An option is in-the-money if it has positive intrinsic value because the market price of the underlying is above {below} the strike price of a call {put}. The reference rate to determine whether an option is in-the-money can be either the spot (in which case the option is said to be in-the-money spot) or the forward (in which case the option is said to be in-the-money forward). If an option is not in-the-money and is not at-the-money then it is said to be out-of-the-money.
Bermudan-style:
An option that can be exercised on a number of predetermined occasions. So, for example, a bermudan receiver swaption would allow the buyer to enter into an interest rate swap as fixed-rate receiver on a number of pre-determined occasions as a hedge for a step-up fixed-rate callable bond in which the bond coupon stepped up annually and the bond was cancellable at each annual coupon payment. Also known as limited-exercise or quasi-American.
Buy-Write:
A covered call position created by simultaneously buying the underlying asset and selling a call option on it. This synthetically creates a short put position – see put-call parity.
Call option:
An option that grants the holder the right but not the obligation to buy the underlying at a predetermined price at or by a predetermined time. The buyer of a call is expressing a bullish view of the underlying and also implicitly, since he is long an option, believes either that volatility will rise or at least that it will not fall. See chapter 8.
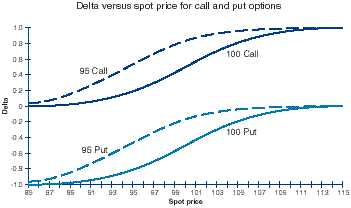
Delta (³): Delta is defined in three, interrelated ways: (i) The rate of change of the value of an option for a given change in the value of the underlying asset. An option with a delta of 0.5 (50%) is expected to change in value 50 cents for every $1 move in the underlying.
(ii) Delta can also be interpreted as a rough measure of the probability of a vanilla option expiring in-the-money: an at-the-money-forward option has a delta of 0.5, since there is an equal probability that the underlying will end up above or below this level. The option therefore has a 50% chance of expiring in-the-money and a 50% chance of expiring out-of-the-money.
(iii> Delta also measures the ‘hedge ratio’ – that is the amount of the underlying asset that needs to be bought or sold to immunize the option to small changes in the price of the underlying. So if if a call option on a particular stock had a delta of 0.5, then 0.5 shares are required to immunize that one call.
For European-style options delta increases in a non-linear fashion from zero to one as an option moves from far out-of-the-money to deep in-the-money. This is because a deeply in-the-money option has a high probability of expiring that way and so will act as a proxy for the underlying, rising and falling in a 1:1 ratio with it. A deeply out-of-the-money option will have little probability of being exercised, so a small change in the price of the underlying will do little to close the gap between asset and strike price. In addition, the closer an option is to the money, the faster delta changes. So for our 0.5 delta call, as the stock price rises the probability that the option will expire in the money rises, so the delta rises, so the more stock has to be bought to immunize the position. This helps explain why a high delta means greater sensitivity of the option price to the price of the underlying: the higher the delta, the greater the replicating portfolio’s stake in the underlying. It also shows how simple option replication requires purchasing the underlying from a rising market and selling it into a falling market.
For interest rate options delta can be calculated with respect to the underlying bond price, with respect to each underlying forward interest rate (as sometimes with cap deltas), or with respect to a small parallel shift in the zero coupon yield curve so that delta is the change in the option price for a small change in all zero-coupon rates. See delta hedging, dynamic hedging, static replication, replication.
Delta hedging:
Delta is the neutral hedge ratio derived from the Black-Scholes model the ratio of underlying asset to options necessary to create the risk-free portfolio that is at the heart of the Black-Scholes option pricing formula. So the delta of a stock option indicates the number of shares needed to hedge a position in an option on that stock for example a portfolio long 100 stock call options with delta of 0.3 is delta hedged by a short position of 30 shares and the delta of an interest rate option indicates the notional amount of interest rate swap required to hedge it against small movements in interest rates. Delta hedging is the application of this concept to the hedging of options portfolios. A true delta hedge is the combination of underlying asset and money market instrument that creates the riskless hedge Black-Scholes says will exactly replicate the pay-off of the option to be hedged. See delta, dynamic hedging, static replication, replication.
Delta neutral:
An option portfolio delta-hedged such that it has no exposure to small moves in the price of the underlying. In practice, since delta is altered by all but the very smallest changes in the price of the underlying, by the volatility of that price, by the maturity of the option, by how close-to-the-money the option is and by interest rates, the ratio of options to underlying must be constantly re-balanced to maintain delta neutrality.
Delta positive:
Call options are said to be delta positive because their value increases by the value of delta for a one unit rise in the price of the underlying. Put options are said to be delta negative because their value decreases in value by delta for every one unit rise in the price of the underlying. This relationship can be upset in barrier options. An in-the-money knock-out call {put} will behave normally until, at a point near to the knock-out, any further increase {decrease}) in the underlying will cause the value of the option to drop because the probability of its being knocked-out is more significant than the fact that it is moving further into the money. At this point puts become delta positive and calls become delta negative.
Dynamic hedging:
Replication of the payoff of a portfolio long the underlying and long a put by continuous delta hedging. It started as a theory of Hayne Leland and Mark Rubenstein on the back of the Black-Scholes model. It was used to provide put protection for equity portfolios at a time when portfolio puts were not available. The theory assumed that an option position could be replicated by continuously adjusting the fraction of funds invested in the underlying equities with the remainder invested in a risk-free asset. An initial hedge of treasury bills was created, its size depending on the level of protection required. If the portfolio value fell, stocks had to be sold and the hedge position increased; the opposite had to be done if its value rose. The theory worked as long as volatility was predictable and low and while markets did not gap dramatically. Since it relied on a large amount of trading in the underlying, it also required liquid markets and low bid/offer spreads. The price discontinuity experienced in the 1987 crash caused such strategies to lose money and credibility. Also known as portfolio insurance. See delta hedging, static replication, replication.
Elasticity:
Properly a measure of the percentage change in the option premium for a 1% change in the asset price. Sometimes loosely used as a synonym for delta (delta strictly measures the absolute change in the option premium for a one unit change in the underlying). Because elasticity is usually significantly positive (a 1% change in the asset price can give rise to more than a 1% change in the option price) it is also sometimes used as a synonym for gearing. This is most common in the warrant market, where it is calculated as delta times the price of the underlying divided by the option price.
European-style option:
An option which can only be exercised on expiration.
Exercise:
Of an option, to put into effect the right to buy or sell at the strike price.
Expected value (EV):
The pay-off of an event multiplied by the probability of its occurring summed over all possible events. For example, the probability of rolling a six on one die is 1¼6 or 16.67%. The EV of a game in which one is paid $100 for rolling a six and nothing for any other roll is (1¼6 x $100) + (5¼6 x $0) = $16.67.
EV is a key concept in option pricing, since the calculation of option value relies heavily on probability theory. The present value of the EV of an option will be the same as its premium if it is fairly priced. The EV of an option is a function of the size of two things: the relevant distribution of probabilities for the underlying asset price (itself determined by time to expiry and volatility) and by the location of the distribution versus the strike price (determined by the relationship between the strike and the current implied forward rate). The former establishes the range of possible outcomes, the latter defines the pay-off value of each outcome. See premium.
Forward intrinsic value:
The intrinsic value of an option plus the basis of the forward underlying it. In an efficient market a European option does not typically trade at less than its forward intrinsic value. An exception is a deeply in-the-money put option where the inability to exercise early and earn interest on the proceeds means that the option’s value is the intrinsic value times the discount factor. This is by definition less than the intrinsic value. See intrinsic value, parity.
Greeks:
The Greek letters used to represent key concepts in pricing derivatives. See delta, gamma, theta, rho, sigma, vega.
Gamma (G):
Mathematically the second derivative of the option premium with respect to the price of the underlying. Gamma measures the change in the delta of an option for a one-unit change in the price of the underlying. If an option has a delta of 0.49 and a gamma of 0.04, the delta would be expected to rise to around 0.53 if the underlying moved one unit in price. (This relationship is made more complex because gamma itself changes with movements in the underlying). Gamma is important to anyone hedging a portfolio of options because it is an indicator of the frequency with which a delta-neutral portfolio should be re-balanced. Gamma is highest for close-to-the-money forward options and decreases the further away from the money the option is. Gamma also increases as volatility decreases for an option which is at-the-money forward. See convexity.
Historical volatility:
The volatility in the underlying’s price, rate or return over a specified period in the past, usually measured as the standard deviation of the natural log of the underlying price relatives. It is used to check whether the implied volatility of an option is cheap or expensive by historical standards. N Ö1/N x S (xi – m) x Ann i=1 Where: xi = log of business daily returns N = total number of business daily returns m = mean of business daily returns Ann = annualization factor
Implied volatility:
The value for volatility embedded in the market price of an option that will equate that market price to the fair or model price of the option. Since option pricing models normally require an input for volatility to derive an option’s price, they can use the market price of the option to derive the level of volatility implied in it. In theory, since the price of options should depend significantly on future views of volatility, the implied volatility should contain some indication of the market’s views of this. In practice option prices are driven by supply and demand factors, themselves heavily dependent on directional views. In general, the higher the implied volatility, the higher the price of the option. Many option prices (particularly foreign exchange options) are quoted in volatility terms, as opposed to ‘live’ price terms.
In-the-money:
See at-the-money.
Intrinsic value:
The amount by which an option is in-the-money and so the cashflow that the holder would realize if he exercised it. It can only be zero or positive, reflecting the asymmetric payout profile of options. [The discounted value of the difference between the strike of an option and the forward. Options struck at-the-money-forward by definition have zero intrinsic value.
Lambda (L):
The change in option value for a small change in the dividend rate (equity options) or foreign interest rate (foreign exchange options).
Limit dependent option:
An option where the payoff is a function of the maximum or minimum achieved by an asset during a reference period. One example is a lookback option.
Option: A contract giving the holder the right but not the obligation to buy {call} or sell {put} a specified underlying asset at a pre-agreed price at either a fixed point in the future (European-style) or at a number of specified times in the future (Bermudan-style) or at a time chosen by the holder up to maturity (American-style). Options are available in exchange-traded and over-the-counter form and can also be packaged as securities either separately (where they are known as warrants) or embedded in bonds.
Out-of-the-money:
See at-the-money.
Parity: Used in several different senses in the warrant and option markets. Of options generally, parity is the condition in which an option’s value in the market is the same as its intrinsic value. In the warrant market though parity can be positive (the warrant has intrinsic value) or negative (it has no intrinsic value). In the convertible bond market, parity is the market value of the shares of common stock into which the convertible can be converted. It is calculated by multiplying the stock price by the conversion ratio. For in-the-money knock-out and digital options, parity is the intrinsic value at the barrier level.
Path-dependent option:
An option whose payoff is a function of the path the underlying rate or price has taken over the life of the option. This contrasts with straightforward European options whose payoff is usually a function of the price of the underlying at only one point: expiry. Path dependent options are typically not priced off analytical solutions and to arrive at a price for the discounted expected value of their terminal payoff over all possible paths, computationally intensive numerical methods are needed. Many non-vanilla options are path-dependent including: average rate options, average price options, average strike options, lookback options, cumulative options, ratchet options, ladder options, digital options, barrier options, shout options and periodic reset options.
Premium:
In derivatives terminology, the amount paid by an option buyer for the option. An option’s premium, technically, equals the probability-weighted sum of all its possible payoffs at expiry, discounted to the present. Option pricing models use formulae to calculate this premium or expected value. Vanilla options are paid for upfront. Many exotic options are paid for in instalments or have premiums whose payment or the timing of whose payment is contingent upon some event. In the UK warrant market, warrant premium is the negative intrinsic value of a warrant if exercised immediately. And in the convertible bond market the conversion premium of a convertible is the difference between the market value of the convertible and its parity value. This is usually expressed as a percentage of parity. See expected value.
Put option:
The right but not the obligation to sell a pre-agreed amount of a specified underlying at a pre-determined price or rate at or by a predetermined time. The buyer of a put is expressing a bearish view of the underlying and also implicitly, since he is long an option, believes either that volatility will rise or at least that it will not fall. See chapter 8.
Put-call parity:
The proposition that the value of a put option is equal to the value of a call option with the same strike price and time to expiration plus a riskless investment of the discounted value of the exercise price and a short position in the underlying. That is, the value of a long call option and short put option both struck at-the-money forward is zero. For European options, an arbitrage opportunity will exist if this condition is not fulfilled since a put purchased alongside a long forward position will synthesize a call and a call purchased alongside a short forward will synthesize a put. Arbitrage prevents the synthetic version of a contract from costing more or less than the original.
Replication:
To duplicate the pay-out of an option by buying or selling the underlying or futures in proportion to its delta. To replicate a call option, the hedger must buy an increasing amount of the underlying if its price is rising and sell increasing amounts if the price is falling because calls are delta positive. The opposite is true of put replication. Volatility and substantial price gapping makes replication difficult in practice. This kind of dynamic hedging is central to the theory of portfolio insurance. See delta, dynamic hedging and static replication.
Rho (R):
The change in option premium for a one percentage point change in interest rates or the discount rates applied to an asset (rho is the Greek letter ‘r’ and ‘r’ is usually the symbol used to represent interest rates). So an option with a Rho of 0.30 USD/% will rise by USD0.30 if interest rates rose instantaneously by 1%.
In general, the higher interest rates are in the denominating currency of the underlying asset, the higher will be the value of the call option and the lower will be the value of a put option. This is because the higher interest rates are the higher the forward price and the lower the present value of the exercise price of an option and so the higher the value of a call and the lower that of a put. In buying a call instead of the asset, the buyer releases capital to be invested in a risk-free asset.
Sigma ():
The annualized standard deviation or volatility of the instrument underlying an option.
Spread:
See chapter one.
Static replication:
In some cases, a complex option can be hedged through portfolios of more standard options designed to replicate, either approximately or exactly, the payoff characteristics of the complex option. In contrast to dynamic hedging the idea of this approach is that the hedge would not have to be changed over the life of the option. For this reason the technique is known as static replication. See delta hedging, dynamic hedging, replication, synthetic.
Strike price/rate/level:
The pre-determined level at which an option can be exercised. For example, the owner of a European-style three-month USD call/JPY put with a strike at 140 has the right to buy dollars and sell yen at an exchange rate of 140 yen to the dollar in three-months time.
Theta (Q):
The sensitivity of option price to the passage of time. The longer the maturity of an option, the greater the value in having the right to exercise or not and so the more valuable the option. The amount of the option’s value that is derived from this phenomenon is its time value and the rate at which this decreases as the option’s life shortens is called theta or time decay. An option with a one-day theta of 0.075 will lose 0.075 of its value as the number of days to expiry decreases by one. Theta is greatest for at-the-money options close to expiry. Theta is closely related to gamma.
Time value:
In options terminology, that part of the premium that is not intrinsic value – that is, the part of the value of an option made up primarily of its time to expiry, strike level and volatility. Time value represents the value of the right to choose to exercise an option against the obligation. The time value of an option decreases at a faster rate the closer it is to expiry.
Vega:
The change in an option’s price for a small movement in volatility. It is expressed either as the absolute change in the value or price of an option for a percentage point change in the standard deviation of the underlying or in points per percentage change in volatility. At-the-money forward options are most sensitive to changes in volatility (their vega is highest) while deep in-the-money and deep out-of-the-money options are relatively insensitive. Options are also more sensitive to volatility the longer their time to maturity.
Vega is important in hedging options positions because implied volatility and therefore the expected hedging costs and value of the options can change, reflecting a change in views about future volatility, without any change in the theoretical price of the underlying. This means that the option premium may change, and so a hedge position may change in value, even if the position is delta and gamma hedged. The total exposure to volatility of a position is measured by the weighted average of vega. A positive vega position is used if a rise in volatilities is predicted and a negative vega if a fall is foreseen.
Volatility:
The measure of how quickly a price varies over time. Annualized volatility is the commonest measure and is usually calculated as the annualized variance or standard deviation of the underlying price, rate or return. Volatility is at the core of all option pricing models because the more volatile the price, rate or return on an asset is, the more likely it is to exceed the option strike price and so the more valuable the option.
Option pricing models differ in their approach to volatility which affects the prices they generate. Black-Scholes and other early single-factor models assume constant volatility. Newer models remedy this error by assuming volatility to be stochastic. This helps explain the volatility smile effect as it increases the value of out-the-money forward options relative to the at-the-money forward options. This is because models that incorporate this assumption allow a greater probability to large movements in the underlying than simpler models. However, as stochastic volatility is a non-traded source of risk, using it as an input into pricing models loses their completeness – that is the ability to hedge options with the underlying asset. Other models assume that the continuously compounded returns of the asset are normally distributed with a variance that is proportional to the time over which the price change takes place. This implies that volatility will increase indefinitely with time. In fact, financial assets exhibit tend to exhibit mean reversion – at a given price extreme it is more likely for the price to move back towards the mean than it is for it to move to a new and more extreme price.
Volatility skew:
The asymmetrical distribution of implied volatility in many markets. Out-of-the-money puts can have higher implied volatilities than calls and vice versa, a fact explained in market terms by supply and demand. When traders talk of trading the skew, they are generally talking about trying to predict the slope of the implied volatility curve plotted against strikes or deltas and choosing an option position that profits if their view is correct. A negatively sloped implied volatility curve implies a negatively skewed probability distribution for the level of the underlying. The skew implied by the Black-Scholes model is zero. In extreme cases the smile can create a two humped or bi-modal probability distribution, unlike the one-humped probability distribution predicted by Black-Scholes. Skew is generally largest in pegged or managed exchange rates where the probability of a large move in one direction is virtually zero, whereas in the other direction it is non-zero or possibly quite large. See risk reversal.
Warrant:
A securitized, generally medium- to long-term, option – often listed on a stock exchange.
Write:
To sell an option.

Comments are closed.