Building an HJM Model in EXCEL – Define calculation cells

2 mins read

Earlier we had defined the input cells for the Heath-Jarrow-Merton (HJM) multifactor no-arbitrage model in EXCEL. In this post we will see how the calculation cells are built up. These include cells for calculating the Brownian shocks, Drifts and Spot and Forward rates.

Brownian Shocks

Brownian shocks to be applied to the volatility factors in the HJM model, dz_i, are obtained as follows. Using Excel’s random function, RAND () we scale the resulting number to the normal distribution by applying the inverse of the standard normal distribution function NORMSINV(). Combined this can be determined in excel using the following formula: NORMSINV(RAND()). These values are derived for each Factor across all time intervals. Whenever the user hits the F9 function button on their key board new results for this formula will be simulated:

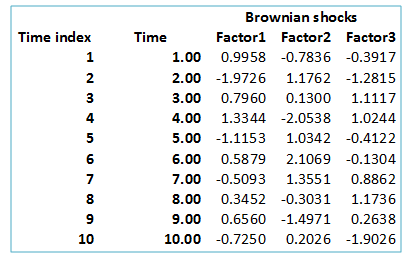
 Drifts

Driftk_t=0.5*dt*( ?_{x =1 to t} Factork_x)² – (?_{i=0 to t-1}Driftk_i), for k = 1, 2, 3  and where Driftk₀=0 and.

Total Drift_t= Drift1_t +Drift2_t +Drift3_t

Spot and Forward Rates Matrix

 

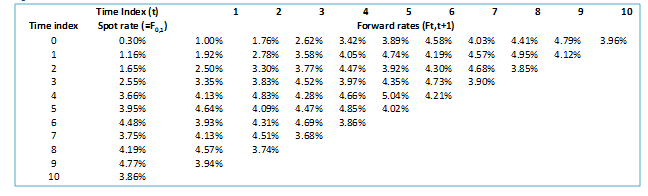
The one-period spot / short rate (=F_0,1) and forward rates (F_t,t+1) are derived using the initial yield curve, Brownian shocks, drifts and scaled volatility factors (Factors 1, 2 and 3) and the following formula:

At time index 0 (as given by the first column in the diagram above) the spot and forward rates are derived using the following formula:

Spot Rate₀= Initial Yield₁ = 0.30%

Forward Rate₀ (t,t+1)=Time Index_t+1*Initial Yield_t+1– Time Index_t*Initial Yield_t , for t = 1 to 10

Where t is the Time Index (as given by the first row in the diagram above)

For example, Forward Rate₀ (1,2)=Time Index₂*Initial Yield₂– Time Index₁*Initial Yield₁=2*0.65%- 1*0.30% = 1%.

(Note this is equivalent to the continuous formula for forward rates e^f(T2-T1)=e^r2T2/ e^r1T1).

At time index 1 and later (as given by the first column in the diagram above) the one-period spot and forward rates are derived using the following formula:

Spot Rate₁ = Forward Rate₀ (1,2)+Total Drift₁*dt+?dt*(Factor1₁*dz1₁+ Factor2₁* dz2₁+ Factor3₁* dz3₁)

Spot Rate₂ = Forward Rate₁ (1,2)+Total Drift₁*dt+?dt*(Factor1₁*dz1₂+ Factor2₁* dz2₂+ Factor3₁* dz3₂)

Spot Rate₃ = Forward Rate₂ (1,2)+Total Drift₁*dt+?dt*(Factor1₁*dz1₃+ Factor2₁* dz2₃+ Factor3₁* dz3₃)

…and so on

Forward Rate₁(t,t+1)= Forward Rate₀ (t+1,t+2)+Total Drift_t+1*dt+?dt*(Factor1_t+1*dz1₁+ Factor2_t+1* dz2₁+ Factor3_t+1* dz3₁)

Forward Rate₂(t,t+1)= Forward Rate₁ (t+1,t+2)+Total Drift_t+1*dt+?dt*(Factor1_t+1*dz1₂+ Factor2_t+1* dz2₂+ Factor3_t+1* dz3₂)

…and so on

Where t is the Time Index (as given by the first row in the diagram above)

For time index 2 to 10 (as given by the first column in the diagram above) the same procedure will be used.

In this post we constructed the calculation cells for the HJM model, in particular cells for Brownian Shock, Drifts including Total Drift and the spot and forward rate matrix. In the next post we will define the output cells for the model and see what the results to the calculation are.