Building BDT model in EXCEL – Define & Set Solver Function & Results

2 mins read

Earlier we had considered how to define the various elements (input, output and calculation cells) of the Black-Derman-Toy (BDT) interest rate model in EXCEL. In this post, we will link all these pieces together by using the Solver Function of the EXCEL worksheet. Once this has been done we will run the Solver Function to arrive at a solution for the median rates and their time varying volatilities (sigmas).

Set Solver Function

The next step in the process is to calibrate the outputs of the model with the inputs of the model. This is done as follows:

In the MS Excel 2007 edition go to the Data Tab and Click on Solver. The following image opens up.

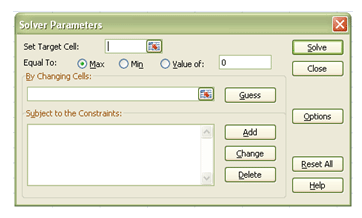
• “Set Target Cell” to the calculation cell for dt.
• “By Changing Cells” will be the cells for the median rates and sigmas, and
• “Subject to the Constraints” will be as follows:

Prices from Lattice = Initial Prices
Yield Volatilities from Lattice = Initial Volatility Rates

 Once these are set, press the Solve button. The Solver function should then calculate a feasible solution for the median rates and the sigmas.

Results

The results of the solver function for our illustration are given below:

(Note: In our illustration the initial and final results are the same as we had already run the solver function prior to this write up.  In reality the initial dummy values may be significantly different from the final results).

In this post, we reviewed how the Solver Function is set up in this EXCEL construction of the BDT interest rate model. In particular, we defined the target and change cells and the constraints with regard to the prices and yield volatilities. After this, we ran the Solver Function which converged to a result for the median rates and time varying volatilities (sigmas). In the posts that follow we will see how these results will be used to price bonds and options.