Earlier we had looked at how the Black-Derman-Toy (BDT) interest rate model may be constructed in EXCEL. In particular, we saw how the median rates and time varying volatilities (sigmas) of the short rate binomial tree were derived. In this post, we will see how these values will be used to construct the complete short rate binomial tree.
We have used the Black-Derman-Toy (BDT) interest rate model to derive six-month short rates. Short rates of interest are future short-term rates of interest that might arise over time and may or may not be equal to the forward rate applicable to that time period (in our case the time period is six months). There are several possibilities of short rates for each future point in time and each short rate has varying probabilities of actually occurring.
We have based our calculations of six-month short rates specifically on the BDT (time-varying volatility) model and worksheets proposed by Mark Broadie and Paul Glasserman at Columbia University.
The BDT model assumes that the short-term interest rates are log-normally distributed (volatility is expressed as a fraction of the current level of rates) with risk-neutral probabilities of an interest rate going up or down in any time period of 0.5. The BDT interest rate tree determined under these assumptions is a recombining binomial interest rate tree.
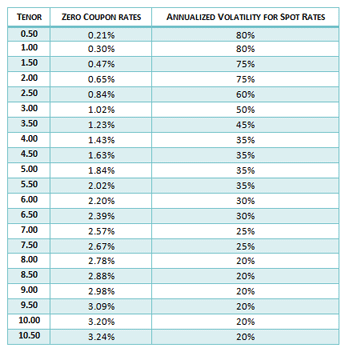
The inputs to this model are the spot/zero-coupon rates and an initial volatility structure for spot rates. The model calibrates the results to these inputs. The initial volatility for spot rates is determined by first calculating the zero curve term structure for each data point in the period, calculating a return series for each rate, calculating the standard deviation for each return series and finally scaling this standard deviation to get annualized volatilities.
Let us assume that we have at our disposal a derived hypothetical zero-coupon (spot rate) term structure and an initial volatility structure for spot rates as follows. The zero rates are continuously compounded rates:
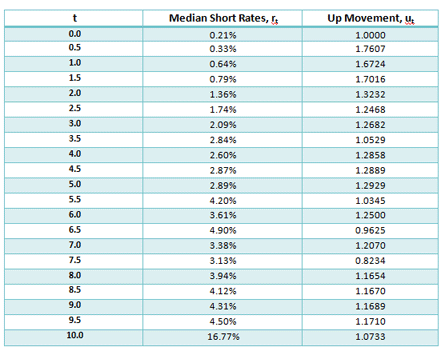
After entering the inputs into the model, median short rates for the twenty periods (or 10 years with 0.5 year intervals) were derived. This is done through calibration of the model’s computed volatility and prices with the observed inputs (i.e. the former are set equal to the latter).
Median rates are rates that lie on the symmetry of the binomial interest rate tree, primarily either equal to the rates on the mid-branch of the tree or the average of the two short rates around the centre. The up movement (u) column is used for generating the entire binomial tree. These short rates are indicative of what the 6-month interest rate could possibly be in the future based on what has been experienced in the past. For example, 1 year into the future the median 6-month short rate has been determined as 0.64% and using the up movements the possible 6-month short rates at that point in time are 1.79%, 0.64%, 2.3%. The short rate binomial tree can be used to price fixed income bonds and interest sensitive securities and derivatives, such as call and put options.
The procedure for generating the complete binomial interest rate tree from the median rates derived is illustrated below for early durations and may be easily extended to generate the full set of short rates:
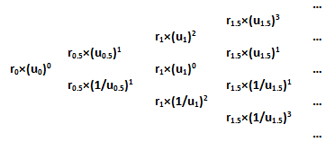
The short rates derived from the BDT interest rate model may be used to price bonds as well as options on bonds.
In this post we looked at how the median rates and sigmas derived using the EXCEL construction of the BDT model were used to build the complete short rate binomial tree. The next couple of posts will illustrate how the rates from this tree will be used to price bonds and options.

Comments are closed.