Commutation functions are an easy, simple and efficient way to calculate the actuarial present value of contingent payments. They are a function of a deterministic survival model and a constant and level rate of return.
The drawbacks of using commutation functions are that they do not work well when decrements have a specific select period, when interest rates vary and when increases in benefits do not follow a regular pattern. With advances in computing power and technology, commutation functions have been replaced by relying on first or basic principles of actuarial mathematics. In addition to the greater flexibility of working from basic principles, calculations based on first principles allow the actuary to work with stochastic models instead of deterministic models thus enabling a more thorough assessment of risk.
However commutation functions are still an effective way of describing actuarial calculations of values of simple annuity and life insurance products, where the values are based on deterministic assumptions of mortality (and other decrements such as turnover, disability, etc) and interest.
The general process for developing commutation functions is depicted in the flowchart below:
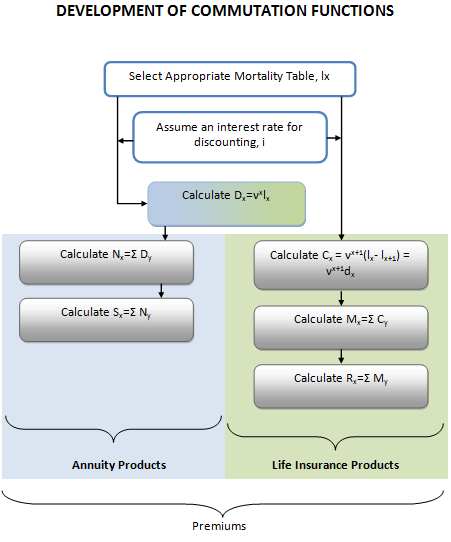
The summations are given from age x to infinity.
For a more detailed discussion on how to derive these functions in excel you may refer to the following post:
Actuarial Mathematics – Introduction to Commutation Functions

Comments are closed.