Actuarial valuation of benefit liability – Defined Benefit Plan
Let us assume Emily is an employee of LifeCorp Inc. which has a gratuity plan that pays a lump sum benefit upon normal retirement age (r) of 60 years. The lump sum benefit is defined as follows:
Retirement Benefit = Final monthly salary per year of service
The salary is assumed to grow at a rate of 8% per annum. For simplicity let us also assume that there are no death benefits for death in service and that there are no other preretirement terminations other than death.
Emily’s details are as follows:
- Date of Birth = 30-June-1980
- Date of employment = 30-January-2002
- Current Monthly Salary = 5000
Sam, an actuary, has been employed by LifeCorp Inc. to determine the actuarial liability as at 31-Dec-2010 and what the suggested funding level for the next year will be for Emily. This suggested funding amount is the Normal Cost. The contribution made by the company can be more or less than the normal cost determined. The amount of normal cost calculated is based on the actuarial funding cost method chosen.
According to IAS 19, the International Accounting Standards dealing with Employee Benefits, the actuarial funding cost or valuation method to be used is the Projected Unit Credit (PUC) Method. Under the PUC methodology the current salary is projected to the retirement date using a salary growth scale. If the unit benefit is the same for each year of service, as it is for Emily, then under this method the projected retirement benefit is distributed evenly over the years of service of the employee.
In order to determine the present value of the defined retirement benefit obligations, i.e. the actuarial liability, the benefit has to be attributed to the current and prior years of service on a prorated basis. The actuarial liabilities are therefore related to the normal cost and therefore also based on the actuarial cost method used.
The first stage in the process is to determine what Emily’s final salary will be:
Age at entry, e = 22
Age nearest birthday on 31-Dec-2010, x= 31
Projected Final salary = Current Salary * (1+8%)60-31=5000*(1.08)29= 46,586
The next stage is to determine the projected retirement benefit/ gratuity amount = Projected Final Salary * No. of years of service:
Total number of years of service = Normal Retirement Age – Age at entry = 60-22=38 years
Projected Gratuity Amount = 46586*38 = 1,770,282
The proportion of projected benefit accrued up to age 31, B31, is:
No. of years since date of entry to valuation date = 31-22 = 9 years
Proportion of projected gratuity benefit accrued up to age 31 = Projected Final Salary* No. of years since date of entry = 46586 * 9 = 419,277
The gratuity benefit that will accrue in the following year based on the PUC method, assumes that the retirement benefit is distributed evenly over the years of service as mentioned earlier. Therefore this unit benefit, b31, will be = Projected Gratuity Amount/ No. of years of service = 1770282/38 = 46,586
All the benefit amounts calculated above (proportion of projected benefit and unit benefit) are applicable as at the date of Emily’s retirement from service. In order to determine their values (i.e. Actuarial Liability and Normal Cost, respectively) the benefit amounts need to be discounted for interest (time-value of money) and mortality. Note that we had earlier assumed that there are no other pre-retirement terminations or decrements. However, in an actual actuarial valuation exercise the actuary may also consider other decrements such as terminations, early retirements, disability, etc.
In order to discount the benefit amounts to the date of valuation we will calculate the following discount factor:
By using first principles:
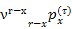
By using commutation functions:
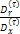
The superscript, (τ), indicates that the function has considered all decrements, which for our example is only termination by death.
Let us assume that the discount rate is 13%. The values of the commutation functions are as follows:

The discount factor thus works out to:


An ample example…Thanx..