We are valuing an FRA for someone who is receiving fixed interest rate payments and who is paying floating interest rate payments.
a. Value of an FRA (zero coupon rate calculated on a discrete basis)
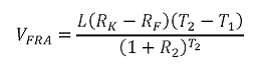
Where, L is the principal amount
RK is the fixed interest rate
RF is the forward interest rate assuming that it will equal the realized benchmark or floating rate for the period between times T1 and T2
R2 is the zero coupon rate for a maturity of T2. In this instance it has been calculated on an effective annual discrete time basis.
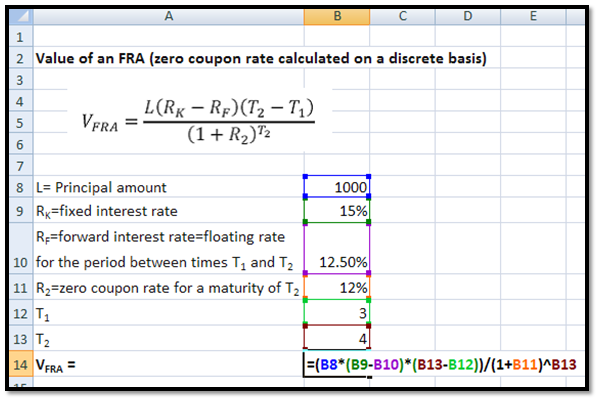
If principal amount, L, is 1000, and we are to receive a fixed interest rate of 15% annually compounded on this amount between the end of year 3 and the end of year 4 and pay a floating rate of 12.5% annually compounded, and the effective annual 4- year zero coupon rate is 12%, then the Value of the Forward Rate Agreement will be:
VFRA =1000 × (15% – 12.5%) × (4 – 3) ÷ (1+12%)4 = 15.89
You may calculate this in EXCEL in the following manner:

b. Value of an FRA (zero coupon rate calculated on a continuously compounded basis)
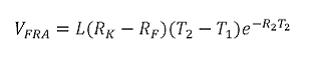
In this instance the zero coupon rate has been calculated on a continuously compounded basis.
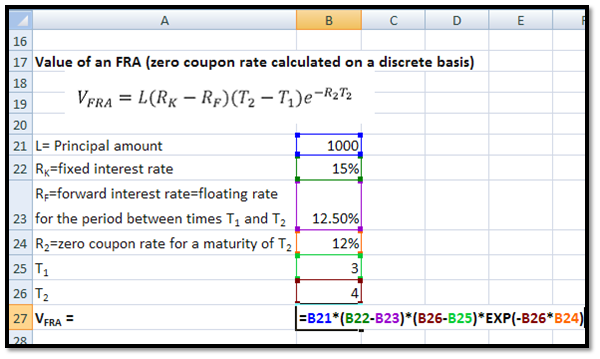
Again if principal amount, L, is 1000, and we are to receive a fixed interest rate of 15% annually compounded on this amount between the end of year 3 and the end of year 4 and pay a floating rate of 12.5% annually compounded, and the continuously compounded 4- year zero coupon rate is 12%, then the Value of the Forward Rate Agreement will be:
VFRA =1000 × (15% – 12.5%) × (4 – 3) × e-0.12×4 = 15.47
You may calculate this in EXCEL in the following manner:

c. How to calculate Forward Exchange Rates
i. Interest Rates compounded on a discrete basis

Where
r is the risk free rate of the domestic currency
rf is the risk free rate of the foreign currency
Suppose that the 1-year interest rates in USD and Pakistan are 2% and 10% respectively. The spot exchange rate is USD 1 = PKR 90.77. The one-year forward exchange rate will be:
F0 = 90.77×[(1+10%)/(1+2%)]1 = 97.89
You may calculate this in EXCEL in the following manner:

Interest Rates compounded on a continuous basis

Suppose that the 1-year interest rates in USD and Pakistan are 2% and 10% respectively. The spot exchange rate is USD 1 = PKR 90.77. The one-year forward exchange rate will be:
F0 = 90.77 × e(0.1-0.02) × 1 = 98.33
You may calculate this in EXCEL in the following manner:



