Risk Exposure. Target Accounts & ALM.
This is the transcript of our last lecture on Risk Management and it completes our online series on Risk Management.
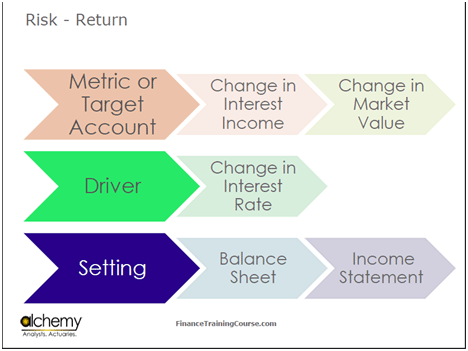
Figure 1 Risk Management – Target Accounts
At the beginning of our first class today, we spoke about target accounts.
In the Banc One case, the target account is tracking two things. One is the change in interest income, and the other is the change in market value or the shareholder’s value. If you look at the Banc One case, it talks about how the market perceives the bank’s strategy, and thus, the market is affecting its share price. The primary driver is the changes in interest rates. The setting includes the balance sheet and the income statement.
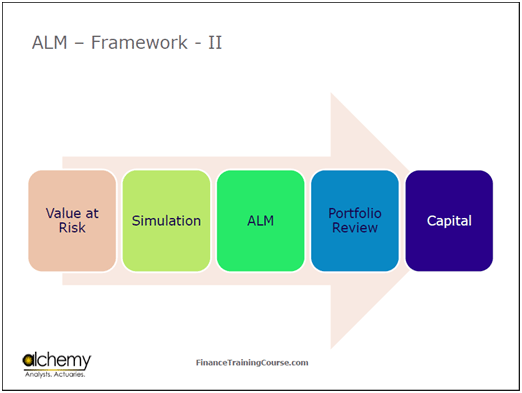
Figure 2 Risk Management. Linking Value at Risk and the ALM framework
How does the Banc One case bring all of this together? If you were to build an ALM model, you would start off right here.
You begin with the Balance Sheet of the bank. You then move to the bank’s Profit & Loss Account(P&L). Next comes valuation. Valuation over here does not mean the valuation of the bank, but rather, of both the assets and the liabilities based on the expected changes in rates. Then there are a bunch of ALM reports which we will talk about in a bit. Next comes the Interest Rate Generator which throws out an interest rate shock. The Calculation Engine then calculates the impact of changes interest rates on the valuations on the Balance Sheet and the P&L as per these reports. Finally, these results are presented.
Recall the Air Canada case. In it, you had a very simple simulation in which you had jet fuel lined expenses, growth and net margin. The item that you were simulating was net margin. In the Banc One case, the bank has made some decisions regarding investments in certain categories and types of assets. These decisions have been made with the funding choices that the bank wants on its balance sheet. It has then hedged a certain portfolio of securities. The Banc One case is a little more complicated in the sense that in addition to understanding the core issue i.e. what has the bank done with its derivative portfolio, you also have to take some time out and understand how banking works in the context of Asset Liability Management (ALM).
Now let’s ensure that we are clear on a handful of terms that will be used in the case later on.
Figure 3 Risk Management. ALM concepts
Sigma– it is the standard deviation or the volatility.
Convexity-Duration is the approximation of a non-linear curve. Convexity is the error term that allows you to compensate for the piece that has been missed out.
Duration– the percentage by which bond prices change due to changes in the interest rate.
Asset Sensitivity– Lets take a simple example to explain this. I have a bank, which has assets of $1000 in each of the following two categories: up to six months, and up to one year. The bank has a liability of $1250 for six months, and a liability of $300 for one year. The gap up to six months in $-250, and the gap up to one year is $+700. The assets earn at an interest rate of 11%, while the bank needs to pay its liabilities at an interest rate of 6%. In terms of the P&L, how much does the bank earn on its assets? In the 6 months case, the bank has more liabilities and hence more deposits. Thus, as interest rates change, the liabilities also change. In the one year case, there are more assets than liabilities. These assets are being funded by two different sources.
Asset sensitivity implies that if a bank’s maturity profile is set in such a fashion that its assets re-price faster than liabilities, it is asset sensitive. If its liabilities re-price faster than its assets, then it is liability sensitive.
When rates are going up, the bank should be asset sensitive. When rates are coming down, the bank should be liability sensitive.
If a bank generates an interest rate outlook, and based on that outlook changes it profile from being asset to liability sensitive or vice versa, this is known as speculation and not hedging. Hedging is the process when a bank locks itself in to eliminate the exposure to a change. In this case the bank isn’t positioning itself to eliminate exposure, but is instead positioning itself in a way to benefit from a change in the interest rate.
Value at Risk– The worst case loss that can occur over a given time horizon and a confidence level.
Banc One is a great case because it shows a bank’s exposures and risk factors. The target account was the earnings account. The impact of changes in interest rates on earnings was discussed, given that the maturity levels of the bank were already mentioned.
The philosophy of running a bank is to borrow at lower rates from stable customers and lend it at higher rates. If the bank also starts paying with its view on interest rates in this mix, it becomes an even more complicated business. The objective of restricting earning sensitivity is to make sure that nobody comes in and plays with the balance sheet to increase short term sensitivity for its own benefit and leave the bank with a much dangerous long term profit.
Do you all understand the concept of an interest rate swap (IRS)? I have a pool of 30 year fixed rate mortgages. I also have a pool of 10 year fixed rate bonds. The bonds would look nice on my balance sheet if interest rates go down, because if interest rates fall by 10%, the price of these bonds would go up by 10 since their interest rate sensitivity is about 10%. But what if I had expected that interest rates would instead go up? The logical solution for me would be to sell these bonds before interest rates go up. However, there are transaction costs which also need to be considered. Also, sometimes, bonds belong to a subsidiary or an associate company, and sometimes have to be there on the balance sheet. So now I am stuck.
This bond throws out a 10% coupon every year. Assume that the notional amount of this bond is US $100 million. Think of this notional amount as the par value of the bond. Also assume that someone else has a bond which throws out a floating rate coupon. To limit my risk exposure, I get into an agreement with this person, and offer him my fixed interest rate coupons in return for his variable interest rate coupons. Both of us do a netting transaction. For example in the first year, the floating interest rate is at 10% while the fixed interest rate was already at 10%. Therefore, no net transaction takes place. In the second year, interest rates have gone up to 12%. The net number is now 2%, and the other party pays me an interest rate of 2% on the notional amount of US $100 million. This exchange happens on every coupon reset date. By doing this, I have created a scenario where I literally sold my fixed coupon bond without actually selling it, and I have acquired a floating rate bond without buying it. Since the coupons have been swapped, this exchange is known as an interest rate swap.
If two floating rate coupons are exchanged, then the swap is known as a basis swap.
Assume that the fixed rate bond discussed in the above example was an amortizing bond in which the notional amount reduced each year. If this was the case, then the floating rate bond belonging to the other company must also be an amortizing bond. If you put in the amortizing schedule into play, you get the Amortizing Interest Rate Swap(AIS).
In most cases, swaps are done with liquid instruments. The rates that are being swapped have very high credit ratings, due to which these rates are very liquid.

