Duration is a measure of how rapidly the prices of interest sensitive securities change as the rate of interest changes (see detailed application example for the banking, insurance and financial services industry in the ALM section). For example, if the duration of a security works out to 2 this means roughly that for a 1% increase in interest rates the price of the instrument will decrease by 2%. Similarly, if the interest rates were to decrease by 1% the price of the security would rise by 2%.
Duration and Convexity together are used to immunize a portfolio of assets and liability against interest rate shock. More advanced applications on the Asset Liability Management front can be see in our Asset Liability Tools note.
Duration is calculated as follows:

Where,
Δi= change in yield (in decimals)
P0= Initial Price
P+= Price if yields increase by Δi
P-= Price if yields decline by Δi
Initial price can be taken as the price on the revaluation date, prior to applying the interest rate changes. The other two prices used in the numerator will also be calculated on this date.
Positive duration is when prices have an inverse relationship with interest rates; when interest rates increase prices decline. This is the case for most fixed coupon, fixed income instruments and for liabilities with reasonably well defined cash flows.
On the other hand, negative duration means that prices have a direct relationship with interest rates increasing when interest rates increase. Instruments that may have negative durations are interest rate caps, long put options on fixed coupon bonds, etc
Floating rate instruments have very short duration due to frequent re-pricing.
Macaulay Duration
This is the weighted average term to maturity of a security’s cash flows. The weights are the present value of the each cash flow as a percentage of the present value of all cash flows. It is given by the following formula:
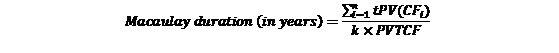
Where k = number of periods (payments) per year
n = number of periods until maturity (years to maturity * k)
i = Period in which the cash flow is expected to be received
PVCFi= Present value of cash flow in the period i discounted at the yield to maturity (YTM)
PVTCF= Total present value of the cash flow of the bond. For calculation carried out on a coupon date this is simply the price of the bond on the coupon payment date (i.e. the clean price or quoted price). For the calculation not on a coupon date, this is the bond’s quoted price plus accrued interest (i.e. the dirty price of the bond).
Modified Duration

For downloadable excel spreadsheets on duration and convexity calculation examples and pdf files on Asset Liability Management and Risk Management, please see the online finance course store.

Comments are closed.