This post presents a working example of Macaulay & Modified duration calculations. Earlier we had considered the importance of the Duration risk metric to Asset Liability Management (ALM) and managing interest rate risk. In this post, we will look at the specific mechanics of the Macaulay Duration and Modified Duration calculations. For application to US Treasuries also see the duration calculation example for US treasuries.
1. Fixed income term sheet
Let us consider a fixed income instrument with the following terms:
Issue Date = 10th December 2010
Face Amount = 100
Tenor = 1 year
Coupon = 10% per annum
Coupon payment frequency, k = semi-annual = 2
Yield to Maturity (YTM) = 12% per annum
The schedule of payments will, therefore, be as follows:
| Date | Tenor | t= Tenor * Frequency | Cash Flow |
| 10-June 2011 | 0.5 | 1 | (10%/2) * 100 = 5 |
| 10-December 2011 | 1 | 2 | (10%/2) * 100 + 100 = 105 |
2. Price
The price of the instrument on the issue date will be the discounted value of the cash flows, i.e. their present value (PVCF). This is equal to:
PVCFt = Cash flow/(1+YTM/2)^(t)
| t |
Cash Flow | Present Value of Cash Flow (PVCF) |
| 1 | 5 | 5/(1+12%/2)^1 = 4.7170 |
| 2 | 105 | 105/(1+12%/2)^2 = 93.4496 |
The price of the instrument at issue is, therefore, the sum of these two present values, i.e. the present value of total cash flow, PVTCF = 4.7170 + 93.4496 = 98.1666
The price may also be obtained directly using the excel formula “PRICE” with the following input parameters:
Settlement = Issue Date = 10th December 2010
Maturity = Maturity Date = 10th December 2011
Rate = Coupon Rate = 10%
Yld = YTM = 12%
Redemption = Face Amount =100
Frequency = k =2
Basis = Type of day count basis = 1 (Actual/ Actual)
3. Macaulay Duration
Macaulay Duration is given by the following formula:
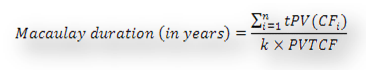
For this instrument, Macaulay Duration works out to:
(1*4.7170+2*93.4496)/(2*98.1666) = 0.9760
The Macaulay Duration may also be obtained directly using the excel formula “DURATION” with the following input parameters:
Settlement = Issue Date = 10th December 2010
Maturity = Maturity Date = 10th December 2011
Coupon = Coupon Rate = 10%
Yld = YTM = 12%
Frequency = k =2
Basis = Type of day count basis = 1 (Actual/ Actual)
4. Modified Duration
Modified Duration is given by the following formula:

Therefore modified duration for the following formula will be:
0.9760/(1+12%/2) = 0.9207
The Modified Duration may also be obtained directly using the excel formula “MDURATION” with the following input parameters:
Settlement = Issue Date = 10th December 2010
Maturity = Maturity Date = 10th December 2011
Coupon = Coupon Rate = 10%
Yld = YTM = 12%
Frequency = k =2
Basis = Type of day count basis = 1 (Actual/ Actual)
In this post, we saw how price, Macaulay Duration and Modified duration were calculated for the sample instrument using both first principles as well as the EXCEL worksheet formulas. In the next post, we will see how Effective Duration is calculated.
Also see Asset Liability Management for Board members – 7 posts, 60 minutes.
xProduct()

Comments are closed.