Treasury Risk reference
Treasury Risk Reference for Risk Metrics, Holding Period Return, Standard Deviation/ Volatility, Annualized Return , Annualized Volatility, Sharpe Ratio, Beta, Treynor Ratio, Jensen’s Alpha, Correlation coefficient, r and Portfolio Volatility taking into account correlations.
1. Risk Metrics
a. Holding Period Return
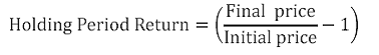
For the calculation of Sharpe and Treynor Ratio(see below) the holding periodreturn derived above is scaled to a year, i.e. to 252 trading days if the holding period exceeds the number of trading days in a year.
b. Standard Deviation/ Volatility
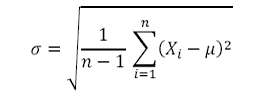
Where Xi is the ith price/rate and μ is the mean (average) of data set, i.e.
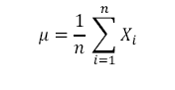 and ‘n’ represents the number of values in the data set.
and ‘n’ represents the number of values in the data set.
c. Annualized Return
![]()
Where the number of trading days in a year = 252 days
d. Annualized Volatility
Where the number of trading days in a year = 252 days
e. Sharpe Ratio
Where RI is the Holding Period Return of investment I.If the number of days in the holding period exceeds the number of trading days in the year the holding period return is proportionately adjusted to arrive at the holding period return for a year.
Rf is the annualized risk free rate of return and ?I is the annualized standard deviation of rates of return of investment I.
f. Beta
Where
ra measures the rate of return of the asset,
rp measures the rate of return of the portfolio of which the asset is a part, and
Cov(ra, rp) is the covariance between the rates of return.
In the Capital Asset Pricing Model(CAPM) formulation, the portfolio is the market portfolio that contains all risky assets, and so the rp terms in the formula are replaced by rm, the rate of return of the market. Rate of return of the broad market index is used as a proxy to the rate of return of the market
g. Treynor Ratio
Where RI is the Holding Period Returnof investment I. If the number of days in the holding periodexceeds the number of trading days in the year the holding period return is proportionately adjusted to arrive at the holding period return for a year.
Rf is the annualized risk free rateof return. The risk free rate is the average rate on a risk free instrument during the period being analyzed.
βI is the beta of investment I with respect to a market benchmark. The market benchmark is usually taken as a broad market index.
h. Jenson’s Alpha
Where
αI = measure of the equity’s performance relative to the respective indices and represents the unique return of the investment.
RIt = The daily return of investment I at time t
Rf = The daily risk free rate of return = (1+annual risk free rate)1/252-1
RMt =The daily returns of the market index at time t
βI = The beta of the equities with respect to the market index
i. Correlation Coefficient, r
Where
n is the sample size
xi is the measurement for the ith observation of x
is the mean of the observations of x
σx is the standard deviation of the observations of x
yi is the measurement for the ith observation of y
is the mean of the observations of y
σy is the standard deviation of the observations of y
j. Portfolio volatility taking into account Correlations
Where
a, b and c are the weights of the respective asset in the portfolio X, Y, and Z are the assets in the portfolio
Variance(X) is the variance in the values of X, i.e. it is X’s volatility squared (σx2)
Variance(Y) is the variance in the values of Y, i.e. it is Y’s volatility squared (σy2)
Variance (Z) is the variance in the values of Z, i.e. it is Z’s volatility squared (σz2)
ρxy is the correlation between X and Y
ρyz is the correlation between Y and Z
ρxz is the correlation between X and Z


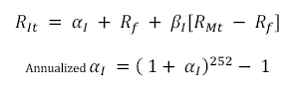
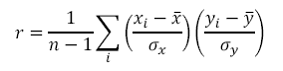

Comments are closed.