VaR Formula Reference
This formula reference includes the following formula, sections and terms related to Calculating Value at Risk. Also see calculating value at risk.
Outstanding term to maturity
(assumes Actual/ 365 day count convention)
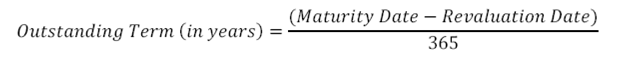
Interpolation
(e.g. interpolation of rates between tenors t and t+1)
Where,
T= outstanding term = t+k years, where t≤t+k≤t+1 and 0≤k≤ 1
Tt=rounded down value of the outstanding term = t years
Tt+1= t+1 years
Rt=Rate observed at time t years
Rt+1=Rate observed at time t+1 years
Rt+k=Interpolated Rate for time t+k
EXCEL’s Price formula
Where:
t = number of days from settlement to next coupon date.
E = number of days in coupon period in which the settlement date falls.
N = number of coupons payable between settlement date and redemption date.
A = number of days from beginning of coupon period to settlement date.
Continuous return of daily prices
Where st is the price at time t and
Rt is the continuous rate of return of the daily prices and is calculated as the natural logarithm of successive prices.
SMA volatility (σ)
Where Rt is the rate of return at time t and E(R) is the mean of the return distribution, i.e.
‘n’ represents the number of return observations used in the calculations.
EWMA volatility (σ)
Where Rt is the rate of return at time t and
λ is the decay factor where(0< λ <1). The industry standard of λ is 0.94.
Weights and Scaling of weights under the EWMA approach
As per the EWMA VaR formula the weight for the data (return) point at time t is:
Where λ is the decay factor where(0< λ <1). The industry standard of λ is 0.94.
The sum to infinity of the all the weights is 1. However it is not possible to have infinite data so if the sum of weights is not close to one, certain adjustments are needed. One option is to increase the number of observations used in the data. The second option is to scale the weights by dividing each weight by the following factor:
Where n is the number of return observations.
Determining daily SMA and EWMA VaR
σ × z-value of standard normal cumulative distribution corresponding with a specified confidence level
Determining the index value for Historical VaR
Index Value = number of return observations × (1-confidence level%)
Scaling daily VaR
J-day VaR= √J × (daily VaR)

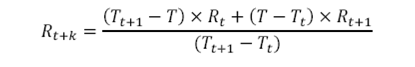

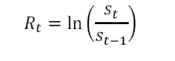
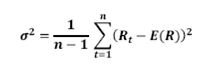
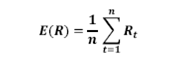
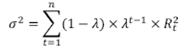
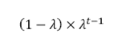
Hi. I needed to drop you a quick nticoe to express my thanks. Ive been following your weblog for a month or so and have picked up a ton of good info and loved the method youve structured your site. I’m making an attempt to run my very own weblog nonetheless I feel its too normal and I have to concentrate on lots of smaller topics. Being all issues to all people shouldn’t be all that its cracked as much as be