Lars Tyge Nielsen provides an interpretation of N(d1) and N(d2) and an explanation behind the difference between N(d1) and N(d2) under the Black Scholes Model. He does this by considering the value of European call option on a stock which pays no dividends prior to the expiry date of the option as given by the following formula:
C= SN(d1) – Xe-rtN(d2)
Where C is the value of the European call option
S is the current value of the stock price
X is the exercise price
t is the remaining time to expiry
r is the risk free rate of interest
N(.) is the cumulative standard normal distribution, the risk adjusted probabilities.
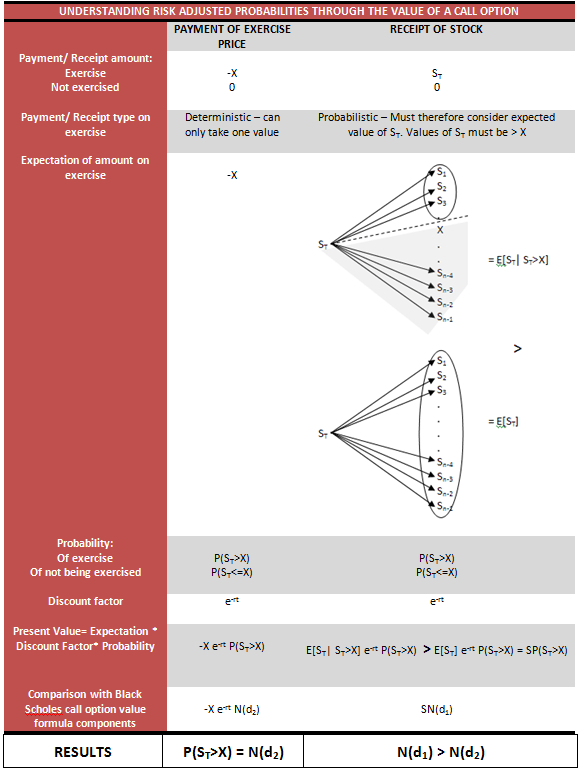
To understand this process, divide the payoff of the call option into 2 components:
- the payment of exercise price
- the receipt of stock.
Both of these are dependent on the option being exercised. This will only occur if the option is in the money. Alternatively, when the stock price on the exercise date, ST, rises above the exercise price, X, i.e. P(ST>X).
Then calculate the expected value and present value of each component:
Payment of Exercise Price and N(d2)
The expected value of the payment of the exercise price is the exercise price times the probability of stock price exceeding exercise price (probability of exercise):
-X* P(ST>X)
Determine the present value of the expected value of the payment by discounting this expected value using the risk free interest rate over the time remaining to the expiry of the option:
-X* P(ST>X)* e-rt
Hence comparing this with the second portion of the call option value equation above, -X* P(ST>X)* e-rt = – Xe-rtN(d2), we see that N(d2) = P(ST>X). N(d2) is the risk adjusted probability of the Black Scholes Model that the option will be exercised.
Receipt of stock and N(d1)
The explanation of N(d1) is a bit more complex. We begin with the expected value of the contingent receipt of stock.
The expected value of the receipt of the stock is contingent on the exercise of the option. It is, therefore, the product of the conditional expected value of the receipt of ST given that exercise has occurred times the probability of exercise:
Statistically, we write this as:
E(ST|ST>X)* P(ST>X)
Or as follows:
E(ST|ST>X)* N(d2)
Note that the first term in this equation is a conditional expectation. It is the expected value of ST given that we are now only considering those future values of ST which exceed the exercise price X. If this constraint were not added we would have E(ST)= Sert the unconditional expectation of ST. Given the conditionality, therefore, E(ST|ST>X) will always be greater than E(ST). We may understand this concept through the following simple probability example.
Simple probability example
Roll a six sided fair die. The probability of rolling 4 is 1/6. Now suppose we have additional information that tells us that the die shows a number great than 3. What is the probability of rolling 4 if we know that the number on the die is greater than 3? The conditional probability works out to 1/3 > 1/6. The conditional probability is higher because we are only considering those outcomes that exceed three in our calculation.
In a similar fashion E(ST|ST>X) > E(ST) because the expected value will only consider those stock prices which exceed the exercise price in the calculation of the expectation. Hence E(ST|ST>X)* N(d2) > E(ST)* N(d2) = Sert*N(d2).
Let us now consider the present value of this expected value by discounting it with the risk free rate over the time remaining to option expiry. We have:
E(ST|ST>X)* N(d2)* e-rt > E(ST)* e-rt*N(d2)= S*N(d2)
Comparing the left hand side of this inequality with the first portion of the Black Scholes equation for the call option, SN(d1), we have:
SN(d1)= E(ST|ST>X)* N(d2)* e-rt > E(ST)* e-rt*N(d2) = S*N(d2)
In other words, N(d1) ensures that the discounted expected value of the contingent stock price received on exercise will be greater than this current value of the stock.
Difference between N(d1) and N(d2)
SN(d1) > SN(d2) ? N(d1) > N(d2)
The risk adjusted probability for option exercise is N(d2). It’s linkage to X suggests that it only depends on when the event ST>X occurs.
On the other hand, N(d1) will always be greater than N(d2). In linking it with the contingent receipt of stock in the Black Scholes equation, N(d1) accounts for:
- the probability of exercise as given by N(d2), and
- the fact that exercise or rather receipt of stock on exercise is dependent on the conditional future values that the stock price takes on the expiry date.
In particular, this means stock prices being greater than the exercise price are taken as a given condition when calculating the expected future value of the stock on the expiry date.
To put this intuition regarding the difference between N(d1) and N(d2) to work within an EXCEL spreadsheet and to build a deeper understanding of the framework, take a look at our newly released video lecture series from our youtube channel.
The video is the fourth video in a series of lectures that builds up the framework presented above and translate it into a discrete EXCEL model. See “An intuitive derivation of N(d2) using the Black Scholes model,” a post the covers an alternate derivation of N(d2) and includes the four video collection in one easy to access location for free.
Reference:

Comments are closed.