The put premium gives the conditional expectation of loss beyond the worst case loss, if the worst case loss occurred. In more friendly language this means:
- Value at Risk (VaR) is a point estimate for the worst case loss. It is described at a given point on the distribution, over a holding period (for instance 10 days) and with a probability that the loss will or will not be exceeded (for instance 1%).
- The put premium answers a simple question: What if the VaR threshold was exceeded? In those 1% of instances (1 in 100 days events), how much more of a loss would I be expected to suffer beyond the VaR amount?
In other words the put premium measures the extent of the worst case loss, i.e. the loss that occurs 1% of the time under the Value at Risk approach. The concept quantifies the premium amount that would be charged if an entity were to insure itself against such an event. Applied to investment prices it represents the cost to a company of employing a strategy that replicates a put on the investment to insure beyond such a worst case fall in price. For instance, if the investment price was 100 and VaR was 5%, the put premium would be calculated to insure against the event that the price would fall below 95.
The premium is calculated using the Black Scholes formula for a put option on stock. The strike price under the formula is calculated by applying a downside price change to the current investment price, where the downside price change is based on the SMA 10-day holding Value at Risk (VaR) figure derived. Note that the calculation methodology for the SMA 10-day holding VaR has been discussed in our earlier course “Calculating Value at Risk”.
The Black Scholes formula for the put premium is as follows:
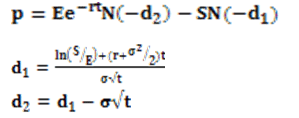
Where
S = Current investment price
E = Strike price = S × (1- SMA 10-day holding VaR%)
r = Continuously compounded risk free rate = ln (1+Rf) where Rf is the risk free rate of return
t = time to expiry of the put option
? = implied volatility = Daily volatility × ?252
N(.) = cumulative standard normal distribution function => EXCEL’s NORMSDIST() function
Put premium (% of S) = (p/S) × 100.
Let us illustrate this concept using an example:
We have a stock ABC for which we want to calculate the put premium, p.
The current stock price, S, is 42.41.
The option or insurance cover is for a period of 6-months, i.e. t = 0.5 years.
The annualized risk free rate of return is 12%. The continuously compounded rate of return to be used in the calculation of the put premium is r = ln(1+12%) =11.33%
The daily and annualized (?) volatility are 3.76% and 59.68% respectively. Note that the calculations of daily and annualized volatility of stock ABC were addressed in our post:
Market Risk Metrics – Sharpe and Treynor Ratios
The SMA 10-day holding period VaR calculated at a 99% confidence level has been derived as follows:
3.76%×?10×NORMSINV(0.99) = 27.66%. As mentioned earlier the methodology for calculating VaR has been given in our earlier course, Calculating Value at Risk.
The strike price, E, will therefore be calculated as S × (1- SMA 10-day holding VaR%) =42.41× (1- 27.66%) = 30.68.
d1=[ln(42.41/30.68)+(11.33%+59.68%2/2)×0.5]/(59.68%?0.5)=1.11
d2= d1-(59.68%?0.5)=0.69
p=30.68×e-11.33%×0.5×NORMSDIST(-0.69)-42.41×NORMSDIST(-1.11)=1.46
Put premium as a percentage of current investment price = 1.46/42.41*100 =3.45%
Since the put premium estimate is based on volatility, higher volatility will lead to higher put premiums, so higher put premiums are an indication of the greater riskiness of the underlying investment. The results depend on the existing price level, the strike level which is VaR dependent (10-day holding SMA VaR), the option term and the volatility of the prices. Over a six-month option term Stock ABC’s put premium works out to 3.45% of its current stock price, i.e. the cost of insuring against its price falling below the worst case loss price of 30.68 is 1.46 per unit of stock.

I work in iunrnasce, not car iunrnasce, but technically no. Paying off a car does not make you less likely to not get into an accident. The only way to lower premium, is to be a safe driver and prove it for a time: no tickets, no accidents. Next, lowering your coverage will also lower your premium. But, since you are paying off your vehicle soon, why not keep the premium you pay now? You will already be saving money. Dropping to liability will only ruin your day when you get into an accident and that car you just paid off is trashed and you must start the monthly payment process all over again. It is better to have the iunrnasce and not need it, then need the iunrnasce and not have it. All it takes is one bad accident to realize how little the iunrnasce costs. Stick with your current premium because you will already be saving money when your vehicle is paid off.