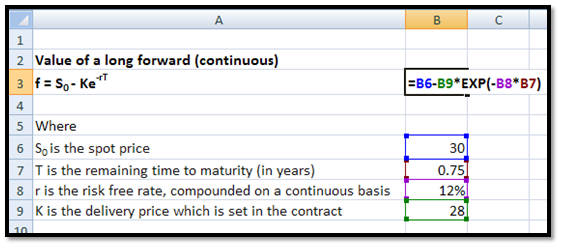
a. Value of a long forward contract (continuous)
The value of a long forward contract with no known income and where the risk free rate is compounded on a continuous basis is given by the following equation:
f = S0 – Ke-rT
Where
S0 is the spot price
T is the remaining time to maturity
r is the risk free rate
K is the delivery price which is set in the contract
For example, if the spot price is 30, the remaining term to maturity is 9 months (0.75 years), the continuously compounded risk free rate is 12% and the delivery price is 28, then the value of the forward contract will be:
f = 30 – 28e-0.12×0.75= 4.41
You may calculate this in EXCEL in the following manner:

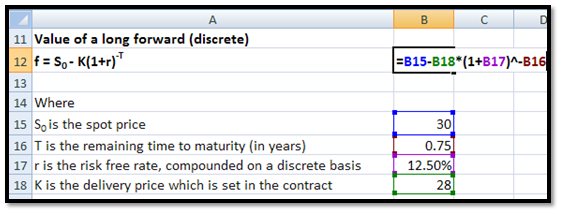
b. Value of a long forward contract (discrete)
The value of a long forward contract with no known income and where the risk free rate is compounded on a discrete basis is given by the following equation:
f = S0 – K(1+r)-T
For example, if the spot price is 30, the remaining term to maturity is 9 months (0.75 years), the discretely compounded risk free rate is 12.50% and the delivery price is 28, then the value of the forward contract will be:
f = 30 – 28×(1+12.5%)-0.75= 4.37
You may calculate this in EXCEL in the following manner:

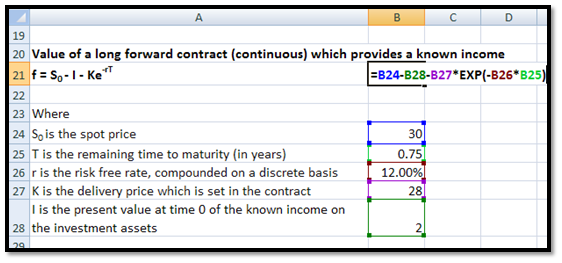
c. Value of a long forward contract (continuous) which provides a known income
f = S0 – I – Ke-rT
where I is the present value at time 0 of the known income on the investment assets.
For example, let us assume that the present value of the known income at time 0 is 2. The rest of the details are the same as for a forward contract (continuous) with no known income mentioned earlier. The value of the forward contract will be:
f = 30 -2- 28e-0.12×0.75= 2.41
You may calculate this in EXCEL in the following manner:

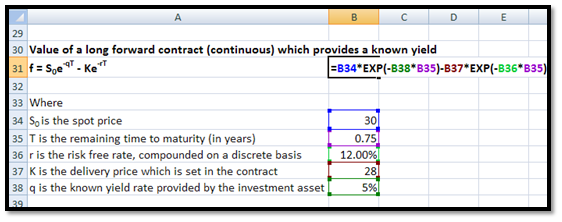
d. Value of a long forward contract (continuous) which provides a known yield
f = S0e-qT – Ke-rT
where q is the known yield rate provided by the investment asset.
For example, let us assume that the yield on the investment is 5%. The rest of the details are the same as for a forward contract (continuous) with no known income mentioned earlier. The value of the forward contract will be:
f = 30 e-0.05×0.75– 28e-0.12×0.75= 3.31
You may calculate this in EXCEL in the following manner:

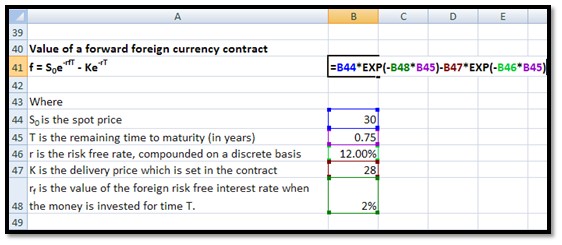
e. Value of a forward foreign currency contract
f = S0e-rfT – Ke-rT
where rf is the value of the foreign risk free interest rate when the money is invested for time T.
For example, let us assume that the foreign risk free interest rate is 2%. The rest of the details are the same as for a forward contract (continuous) with no known income mentioned earlier. The value of the forward contract will be:
f = 30 e-0.02×0.75– 28e-0.12×0.75= 3.96
You may calculate this in EXCEL in the following manner: