To demonstrate how to calculate Duration and Convexity for specific US Treasuries we select instruments from recent US Treasury bill, note and bond auctions. Please note that we are determining these metrics (Convexity & Duration) at issue. We will calculate Macaulay, Modified and Effective Duration as well as Convexity for the selected Treasury issues.
You can use the approach to build your own EXCEL calculator.

You may first want to review our course on duration & convexity calculation example to become familiar with the formulas & mechanics of the calculations before proceeding.
1. Duration and Convexity calculations for T-Bills
a. Prices & Yields

According to the Federal Reserve Bank of New York, T-Bills “are quoted at a discount from face value, with the discount expressed as an annual rate based on a 360-day year“. Calculate the price (per $100) at issue date, therefore, as 100*(1-T/360*0.14%) where T is the number of days between the maturity date and the issue date, in this case, 364 days.
So we have 100/(1-364/360*0.14%) = 99.858444
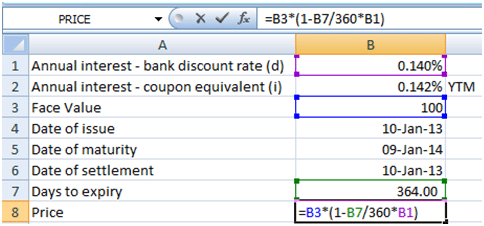
As you can see this tallies with the price mentioned in the auction results.
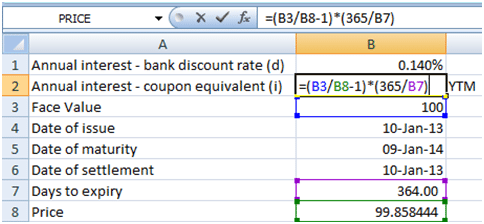
The investment rate is the coupon equivalent yield. This yield is the annualized percentage return that the purchaser will receive if the note is purchased on the day of the quotation at the ask price and held until maturity. For a redemption value of the bill of $100, and the ask price of 99.858444 we calculate the coupon equivalent yield (i%) as:
99.858444*(1+i%*364/365) = 100
Therefore i% = (100/99.858444-1)*365/364 = 0.142%
b. Macaulay Duration
Macaulay Duration is the weighted average time to maturity where the weights are the present values of future cash flows. In the case of a T-Bill there is only one cash flow that is due on the maturity date, the present value of this cash flow on the issue date, therefore, is equal to the price of the T-Bill. Hence the Macaulay Duration for a T-Bill will be equal to the time to maturity (expressed in years), in this instance 364/365 =0.9973.
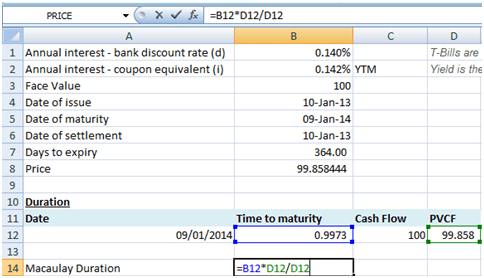
The same result for Macaulay Duration may be obtained using the EXCEL’s DURATION function with settlement date = issue date = 10-Jan-2013, maturity date = 9-Jan-2014, Rate = 0% (as bills are zero coupon instruments), Yield = 0.142%, frequency = 1 and basis (day count convention) =3 (i.e. Actual/365).

c. Modified Duration
Obtain Modified Duration by making an adjustment to Macaulay Duration. In particular Modified Duration = Macaulay Duration/(1+yield %/frequency) = 0.9973/(1+0.142%/1) = 0.99584.

Again, the result may be obtained directly in EXCEL using the function MDURATION with settlement date = issue date = 10-Jan-2013, maturity date = 9-Jan-2014, Rate = 0% (as bills are zero coupon instruments), Yield = 0.142%, frequency = 1 and basis (day count convention) =3 (i.e. Actual/365).

d. Effective Bond Duration
Effective Duration is a measure of the interest rate sensitivity of the price of the instrument to small changes in the interests. It is given by:
(P– – P+)/(2*P0*(absolute change in yield%))
where P– is the price of the bill if the yield rate were to decline by a small amount (in our example 0.10%) and P+ is the price of the bill if the yield rate were to increase by the same small amount. P0 is the price of the bill at the current yield%. The current yield as mentioned earlier is 0.142% so given the % change in yields, the increased yield is 0.242% and the decreased yield is 0.042%.
Calculate the prices using the coupon equivalent yields as follows:
100/(1+i%*364/365).
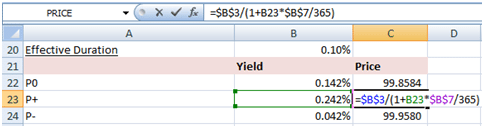
With effective duration calculated as given in the image below:

The effective duration, therefore, works out to 0.9958.
e. Convexity
Duration ignores the curvature of the price-yield function. It may therefore over- or under-estimate the price change when interest rates change because it presumes that prices will be impacted by the same extent whether interest rates increase or decrease. The convexity measure aims to correct this deficiency in the duration metric. Calculate the effective convexity as follows:
(P– + P+-2*P0)/(2*P0*(absolute change in yield%^2)), where prices are defined as mentioned earlier for the effective duration.

The effective convexity, therefore, works out to 0.9917.
f. % Change in Price
What is the % change in price if interest rates increase by 0.10%? The answer is given by the following formula:
-Duration * change in yield% + Convexity *(change in yield%^2)
Note in this instance we are taking the actual change in yield and not its absolute value.
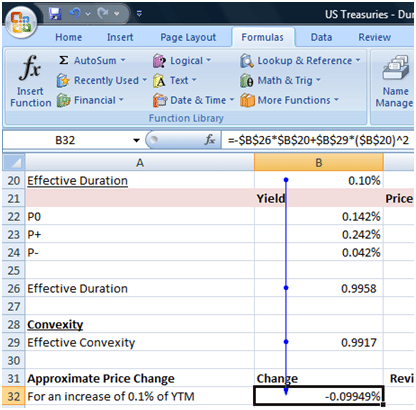
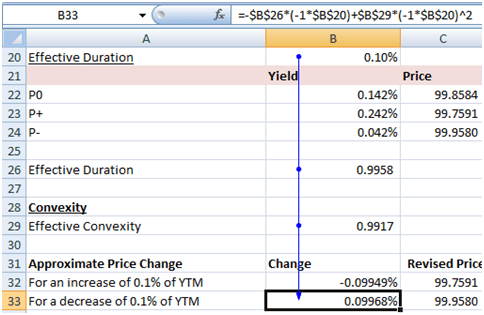
An increase of 0.10% in the yield rate would cause prices to decline by 0.09949%. While a 0.10% decline in yields would result in a price increase of 0.09968%.
2. Duration and convexity calculations for Treasury Notes and Bonds
a. Prices & Yields

The price for the 5-year Note determined above may be calculated in EXCEL using the PRICE function with settlement date = issue date = 31-Jan-2013, maturity date = 31-Jan-2018, Rate = 0.875%, Yield =0.889%, Frequency =2 (for semiannual coupon payments) and day count convention =1 (Actual/Actual).
We may also determine the price using first principles. Strip each future coupon and principal cash flow and discount each of them to the issue date using the yield rate.
Use the same methodology as for notes to determine the price, duration, convexity & sensitivity for the 30-year Treasury Bond.
According to the Federal Reserve Bank of New York, “note and bond prices are quoted in dollars and fractions of a dollar … [where the] fraction used for Treasury security prices is 1/32“.
To convert these prices into the quoting convention we may use the following approach:

Where 99.298138 in quoting convention is equivalent to $99.931681 (=99+29.8138/32).
b. Macaulay Duration
Notes and Bonds have periodic coupon payments. To calculate the Macaulay duration first strip each payment and calculate its present value to the settlement date (in this case the issue date). Multiply each present value with its corresponding time to maturity in years. Sum the derived products and divide this sum by the total of the present values (i.e. the price). The resulting figure is the Macaulay Duration – the weighted average time to maturity (in years) with weights as these present values.
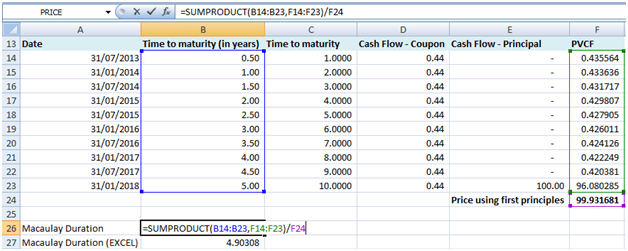
Macaulay Duration using EXCEL’s DURATION function will also give the same answer without requiring the user to calculate the present values of each cash flow [with settlement date = issue date = 31-Jan-2013, maturity date = 31-01-2018, Rate = 0.875%, Yield =0.889%, Frequency =2 and day count convention =1 (Actual/Actual)].
c. Modified Duration, Effective Duration & Change in Price
The methodologies for Modified Duration, Effective Duration and % change in price (sensitivity) are similar to the method we use for bills. For Modified Duration calculated using EXCEL MDURATION function use settlement date = issue date = 31-Jan-2013, maturity date = 31-01-2018, Rate = 0.875%, Yield =0.889%, Frequency =2 and day count convention =1 (Actual/Actual).
Download the Duration and Convexity for US Treasury Bill, Note and Bond EXCEL file for free!
