How does the EXCEL DURATION calculation work? How do we calculate it for settlement dates between coupon dates? This is a common question that our readers pose. We have already examined the calculation of Excel Duration and Price functions when the settlement date equals a coupon payment date in our earlier posts:
In these posts, we demonstrate how to calculate duration from first principles and how the results tally with numbers generated using EXCEL DURATION (for Macaulay Duration), PRICE & MDURATION (for Modified Duration) functions.
Now we will look at an instance where the settlement date falls between coupon payment dates.
EXCEL duration calculation – The PRICE function
When we calculate the price of a note or bond on a date other than a coupon paying date or an issue date, the price quote may either be a clean price or a dirty price depending on whether we exclude accrued interest from the calculation or not. EXCEL’s quoting convention for PRICE is the clean price of the bond . That is, it subtracts the accrued interest out from the sum of the present value of future cash flows. You can see this when you click the “Help on this function” link for EXCEL’s PRICE function. The last part of the given formula is the accrued interest (in a red box below):
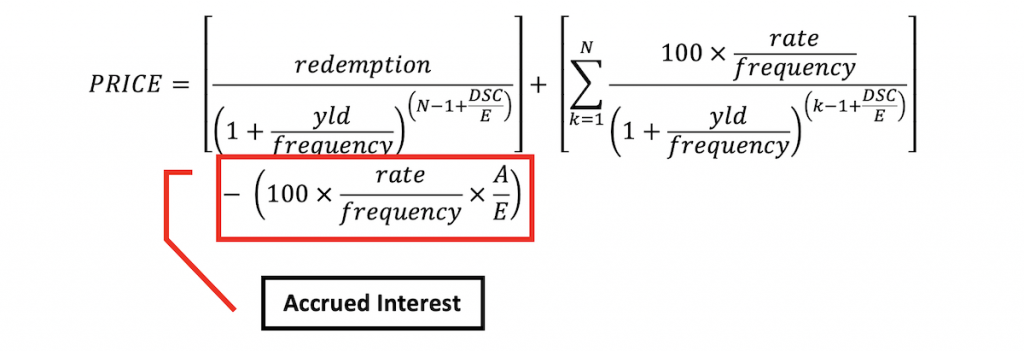
EXCEL Duration Calculation – Macaulay DURATION
However, the calculation of EXCEL’s DURATION does not factor out accrued interest.
Recall the formula for Macaulay Duration:
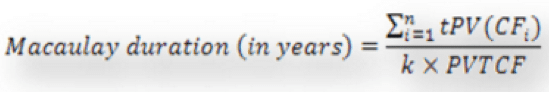
In the numerator PV(CF1) is the present value of the cash flow due at the end of the initial period which contains the settlement date. This cash flow will consist of the coupon payment and/or the principal payment, if applicable. The interest earned for the period between the period start date and the settlement date will not be deducted from the present value of this cash flow.
Likewise in the denominator, PVTCF (Present Value of Total Cash Flows) is equivalent to the dirty price of the bond and not its clean price. If we use EXCEL’s PRICE function to determine the denominator for the Macaulay duration we need to add back the accrued interest.
Settlement date equals coupon payment date
Let us look at an example of a five year note with the following terms:

On a coupon payment date of 31-July-2016, there is no accrued interest. The clean price will equal the dirty price of the note, i.e. 99.979185.
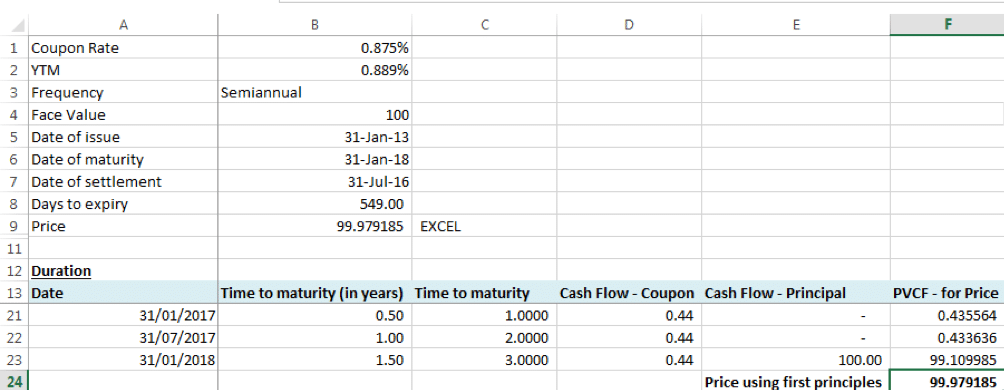
Macaulay Duration from EXCEL equals 1.49347. See the calculation using first principles in the screenshot below.

Because accrued interest is zero, the present values of cash flows (PVCF) for calculating price and the Macaulay duration in each period are the same.
Settlement date does not equal to a coupon payment date
Now let us consider the settlement date of 14-November-2016 which falls between the coupon payment dates of 31-July-2016 and 31-January-2017 respectively.

In this case, we can see a difference between the cash flows in the initial period which contains the settlement date i.e. 31-July-2016 and 31-January-2017. The PVCF for Price calculation in this period is reduced by the accrued interest earned between 31-July-2016 and 14-November-2016. Accrued interest = 100 x 0.875%/2 x A/E = 100 x 0.875%/2 x 106/184 = 0.252038. There is no similar deduction made in this period for PVCF for the duration calculation.
In row 24, Price in the “PVCF – for Price” column is the clean price of the note, while the figure in the “PVCF – for Macaulay Duration” column is the dirty price of the note. As mentioned above, Dirty Price = EXCEL PRICE + Accrued Interest = 99.982924 + 0.252038 = 100.234962.
Macaulay duration on 14-November-2016 is 1.20543. Accrued interest is not subtracted from the initial period PVCF in the numerator and dirty price in the denominator.
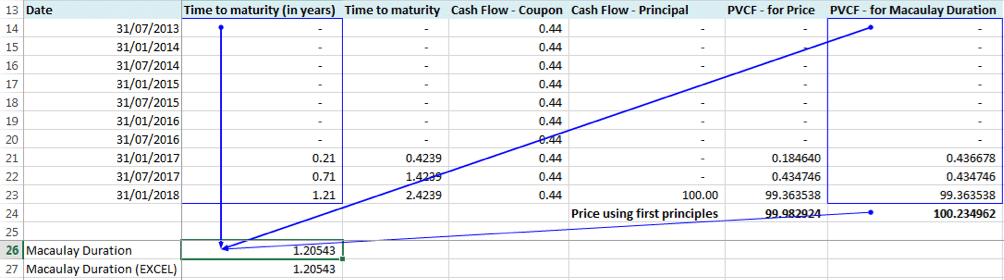
The value derived from the first principles matches the value obtained using EXCEL’s DURATION function.
