This weekend while teaching the portfolio management and optimization course to a group of Executive MBA students at IBA we ran into an interesting debate on calculating annual returns, holding period returns and aggregate returns for an equity portfolio. We realized that because of difference in market practices across the region we take a great deal of calculations for granted.
The questions around actual realized returns arose when we started discussing performance evaluation and interpreting fund management and performance reports filed by fund advisors, mutual funds and investment management professionals. If you are fund manager why would you favor one return calculation over another and what is the difference? Why is there a difference between the returns that we calculate and the returns quoted in the fund management reports? As an investor sitting across the stable would you prefer the same standard or an alternate one?
I thought it would be useful to do a short review that walks us through a simple example and the three possible choices of calculating and quoting returns that you are likely to come across.
The settings for the question.
Our original class discussion case focused on an equities only portfolio. We take the same example for illustrating the procedure used for calculating holding period return, aggregate return and compounded annual returns.
We have an equities only portfolio that is invested in 12 securities.
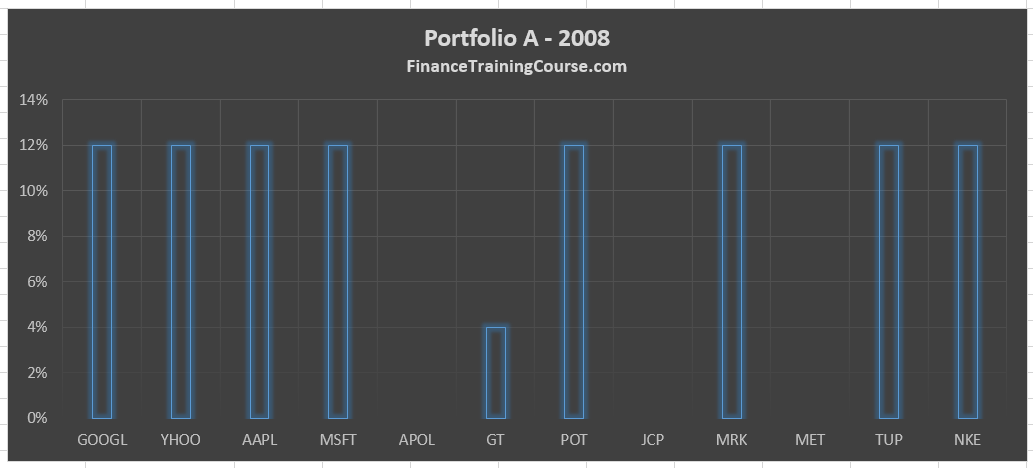
The original amount invested on 1st December 2008 was US$ 29,932.6. The primary constraint on the portfolio was a per security limit of 12% of total portfolio investment with rebalancing. This means that every six months the portfolio was reviewed and exposures of above 12% were reduced to 12% and exposures of below 12% were increased to 12%. Dividends were reinvested back into the same positions.
On 15 November 2012 portfolio performance was reviewed after a period of four years. The value of the portfolio stood at US$ 73,074.4. What was the total holding period return across four years? What was the annualized return per year for each of the four years?
We will now answer this question using three related but slightly different approaches.
Aggregate return and annual return using simple interest.
The aggregate return calculation is easy. We calculate the change in the value of the portfolio and express it as a percentage of the original invested amount.
Aggregate return = (Ending portfolio value – beginning portfolio value)/(beginning portfolio value)
Total return = (73,074.4 – 29,932.6) / (29,932.6) = 144.2%
The return per annum calculation is where two of the alternates diverge.
The first approach – the simple interest approach – divides the aggregate return by the holding period expressed in years to get the annual return figure.
Our holding period is 1,445 days. Divided by 365 and expressed in years that gives us 3.96 years.
The simple interest approach divides 144.2% by 3.96 years to give us a 36.4% return per year or:
Annual return = Total return / holding period in years
How do we know that this is the correct answer? We can reconcile the return with the portfolio ending value by plugging in the return in the following equation:
Ending portfolio value = Beginning portfolio value * (1 + 3.96 * 36.4%)
If the calculated return is correct the ending portfolio value from this equation should reconcile with the actual ending portfolio value in our account.
We refer to this approach as the simple interest approach because we assume no compounding of interest or returns.
To re-emphasize, our 144.2% aggregate return translates into 36.4% annual return per year without any compounding of returns across the four years.
Aggregate return and annualized return using compound interest.
If we want to express the same return using compounding of returns the calculations change slightly. This is the second approach. The aggregate return remains the same. So our starting point is the same 144.2%
To calculate the annual return per annum using the compounding approach we need to follow a two- step approach. We need to first gross up the returns. So our 144.2% will become 244.2%
To estimate the annual compounded return we plug in the aggregate return in the following equation
Annual compounded return = (1 + aggregate return) ^ (1/holding period in years) -1
Annual compounded return = (1+144.2%) ^ (1/3.96) – 1 = 25.3%
How do we know that this is correct? Once again we can reconcile the results using our compounded return equation
Ending portfolio value = Beginning portfolio value * (1+annual compounded return)^(holding period in years)
When we plug in the correct values our ending portfolio value reconciles with the original value
73,074.4 = 29,932.6 * (1+25.3%)^(3.96) = 73,074.4
Aggregate return and annual return using continuous compounding
Our third and final approach is the one that causes the most confusion. Sometime we calculate or observe results quoted on a continuous compounded basis. How does that work?
First the aggregate return calculation is different and throws out a different number. To calculate returns on a continuous compounding basis we use the following formula
Aggregate return = LN (Final portfolio value / beginning portfolio value)
Aggregate return = LN (73,074.4/29,932.6) = 89.28%
To double check and reconcile the results use the following relationship
Ending Value = Beginning value * exponential (return)
73,074.4 = 29,932.6 * exponential (89.28%)
To calculate the annual continuously compounded return use the following relationship
Total return = Annual return * holding period in years.
Or
Annual return = Total return / holding period in years.
Did you notice we have come full circle?
Both the simple interest approach and the continuous compounding approach use the same model to calculate annual return. However because the underlying model is different the results are different.
Here is quick summary of our results:

The big question. Which approach do you prefer?
As a fund manager, the simple approach for calculating and quoting annualized returns or returns per annum is very attractive.
It is easy to explain, easy to calculate and its looks better than the other two alternates. As an investor though we often look at multiple asset classes including bonds and currencies where returns are quoted on a compounded basis. So a 36.4% return on a simple interest basis is not really comparable with a 25.3% return quoted on an annual compounding basis. In general, we rarely see performances or returns quoted on a continuous compounding basis but it’s a useful measure to have in certain instances. So as an investor the preference is to see some compounding in return in order for us to make meaningful comparisons across asset classes.
Most securities regulators understand this and regulate both fund disclosures and fund manager reports. The objective is to standardize reporting across an industry so that investors are not mislead or misinformed because of usage of different investor reporting standards across the industry.
