There is one question that I ask myself every time I am about to make an investment decision. Is the amount I am allocating and committing to this investment too large? Can we afford the size of this bet? Is this a mistake? Will there be regrets later?
I asked myself this question before I put down the buy order for my first trade, deposit for our first car, lease for our first apartment, capital for our first venture and the down payment for our first office. Over the years as I made these decisions, I wondered if there was a framework, a criterion that I could use or look at to get my answers faster. Later, as bets grew bigger and decisions came faster, I wondered what sort of a model my intuition was building and using. I also wondered if there was a theoretical basis for my actions.
It turns out there is. The right approach is always to focus on the question we want to answer. The question we want to answer varies depending on what we want to achieve. Minimize risk? Balance risk and reward tradeoff? Maximize capital base? Optimize our wealth at the end of the investing cycle? Maximize the growth rate of wealth? Your trading strategy is a function of what you want.
A common theme across these perspectives and questions is bet size. How do we minimize risk? By reducing exposure (bet size) to riskier assets. How do we balance risk and reward tradeoff? By estimating the return per unit of risk an allocating capital (bet size) to positions using it as a metric. How we maximize capital? By preserving it using stop loss and other trade management tools to close loss-making positions (bets).
If we treat a trading strategy as a multiperiod game with the rate of growth of wealth as the objective that needs to be maximized, what is our best way forward? Turn out one of the answers is bet size. Kelly’s criterion, Kelly’s formula, Kelly’s bet and Kelly’s strategy all refer to the seminal paper written by J. L. Kelly, Jr. in 1956 that explored the relationship between the rate of growth of wealth and bet size. While the initial application of Kelly’s criterion was focused on betting and gambling, the framework has been extended to many other applications.
Why haven’t you heard of Kelly?
Introductory texts on portfolio management and optimization don’t cover Kelly. There are many reasons for that. Kelly’s Criterion original focus was on gambling games with bets repeated with the same odds. Translating the framework to multi period portfolio allocation across a universe of securities required some work. There were also issues with accurately estimating odds and edges for a universe of securities. Under certain circumstances Kelly’s optimal bets were considered to be larger and riskier in the short term. More importantly, it is only when you start looking at multi period optimization that you start to come across Kelly.
As seasoned investors and traders, it is impossible to not come across Kelly criterion or ideas based on Kelly. Do a google search on trading and bet sizes and four out of ten results on the first page refer to Kelly in some shape and form. Thanks to work done by economists, academics and traders there are implementations derived from Kelly’s criterion that can be applied to investments in equities.
The size of your bet?
The simplest and crudest presentation of Kelly is edge over odds. The edge is the amount you are likely to win on average over multiple bets. The odds are the assessment or likelihood of that win. If your edge is 20% (you are likely to book a gain of 20%) and the odds are even or fair (you have a 50% chance of winning or losing), according to Kelly your optimal bet size is 8.3%. (See the section at the end on the math for Kelly’s criterion if you want to run the numbers yourself.)
How would optimal bet sizes vary with changes in the probability of winning and edge? If the odd were in your favor (80% chance of winning) and your edge stood at 1.2, should you bet the entire bank or only part of your capital? The table below presents optimal bet sizes based on Kelly for changing values of edge and odds.
The vertical index lists a scale of probabilities that goes from high to low as we move from top to bottom. These figures represent the probability of winning the bet. the horizontal index lists increasing edge as we move from left to right. The numbers listed in the table represent estimated bet sizes using Kelly’s criterion for each cell. For instance with a 60% probability of winning and 1.5 edge, the recommended Kelly’s criterion bet is 33% of your bank roll.
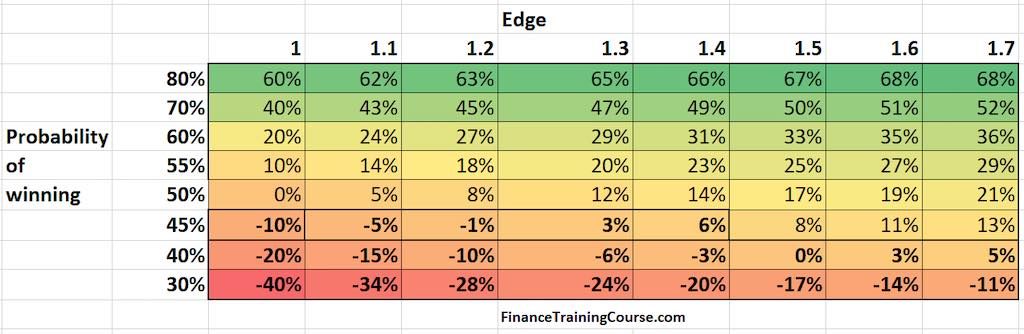
The color coding shows areas of strong promise (shades of green), neutral (between lime green and yellow) and unfavorable (ocher and hints of red to red).
Even the best odds (80% chance of winning) and a reasonable edge (1.4) lead to a bet size of 2/3 of your capital. Remember under Kelly the objective is to not maximize expected payoff but growth in capital. Growth in capital over multiple bets or seasons has a central condition – survival. If you have nothing left to bet, if you have depleted your capital, you are out of the game.
The next time you come across a sure thing, you know what to do.
Hold a part of your capital back, don’t bet the boat. Capital preservation, not accumulation is the key to maximizing wealth over a multi period investing time horizon.
Fully Kelly, fractional Kelly and boundary conditions.
Just because Kelly suggests that you should bet 40% of your pool of capital, should you? The answer is no.
Your estimates of odds and edge are most likely inaccurate and off. Your objective function and utility may require a different mindset. While we often see statements indicating that a Kelly strategy will outperform all other strategies over time, the required time duration for Kelly to outperform other strategies may surprise you. Depending on the value of parameters that define your market and your bet, the time required for Kelly to outperform all other strategies with a certain degree of confidence may range anywhere from 80 years to 200 years.
Which brings us to fractional Kelly strategies. Models that don’t be the entire amount recommended by Kelly but some fraction. Opinions are mixed on how effective the approach is but there is consensus that a fractional Kelly approach leads to lower short term risk at the cost of giving up potential upside.
A second element is rebalancing and fixed portfolio weights. Both help with performance over multiperiod investment horizon but add to transaction and execution costs. They are not a nice to have. They are required and lead to better performance when compared to strategies without rebalancing. Your original strategy and allocated weights go out of alignment as soon as any one position outperforms the others. You have to rebalance your positions (adjust actual dollar value by buying and selling) to get the weights back in alignment.
What drives or dominates the determination of bet size? Is it the probability of winning (your odds) or the pay off (your edge)?
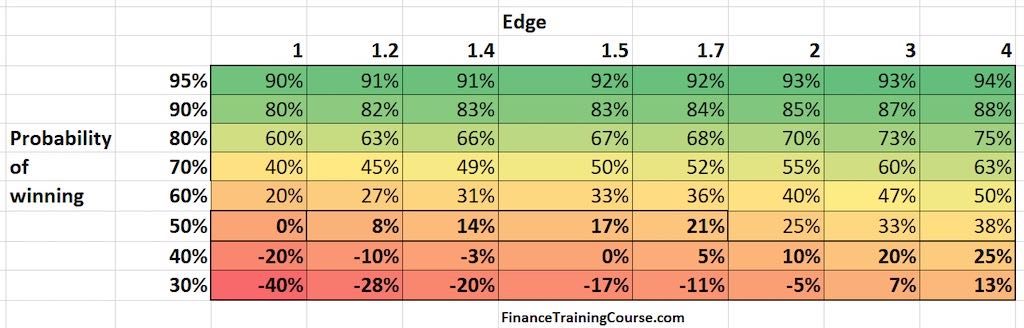
The answer is the probability of winning (or conversely not winning) rather than edge. At higher probabilities of winning, an increase in payoff will only result in a slight increase in your bet size. Kelly is not going to recommend that you bet the entire bank. The model would still suggest that you hold some capital back. According to Ziemba (2012), the relationship between bet size and edge is linear in nature where as the one between bet size and odds or probability is clearly non-linear.
At lower odds, it would take a significant increase in payoff for Kelly to recommend that you put capital at risk. Favorable odds with lower edges still result in a recommendation for capital allocation, albeit small amounts, under Kelly. So do massive payoff (an edge of 4 – a 400% return) with unfavorable odds (30% chance of winning, 70% chance of losing). But remember the qualification above. It is likely that your estimates are off and have a strong bias towards a direction that would make you commit to the bet.
Startups, Founders and Kelly’s Criterion
An example may help understand the point being made.
How could we apply Kelly’s criterion to startups and founders. Specifically risk taking behavior of founders. Founders often use explicit or implicit leverage to raise financing using bootstrapping, credit cards, friends and family funds, angels or venture capital or quite often a combination of all of the above.
In most instances, founder estimates of odds and edges are based on their read of an opportunity and a market with significant execution and delivery risk. Ideally, significant payoff with terrible odds under the best of conditions. Hyper inflated projected payoff (unreal and not likely) with terrible odds under more common conditions. How do you allocate capital, time or commitment to an idea where not just the odds, but the assessment of odds is also off?
As per our updated bet size table below anything less than a 13% probability of winning shouldn’t be allocated capital. At lower odds even when capital is allocated, it is limited to less than 1% of pool of available funds. Compare this with founder behavior you have witnessed and you will see that actual observed bets are opposite of those suggested by Kelly. Founders often end up making out-sized bets when faced with terrible odds.
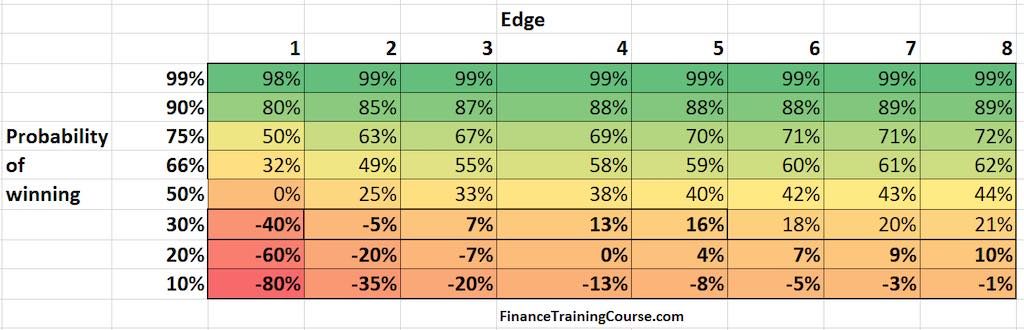
How can we explain this behavior?
The easiest explanation for founder behavior is to discount usage of Kelly. Founders don’t use Kelly’s criterion or are not aware of it. An alternative explanation is the disconnect that exists between founders’ view of the world and reality – also known as the reality distortion field. Founders have a different view of odds and payoffs. The rest of the world may see red, they see bright green. Still with best of odds and best of payoff under the model above Kelly doesn’t recommend leverage. But we know that founders use leverage across financing choices. There are conditions in the capital market where Thorp does suggest the usage of leverage, but those conditions don’t apply to most founders.
There is a third view. Successful Founders understand survival and failure rates. They are aware of the multistage nature of the startup game. Founders are gamblers at heart and understand Kelly at an intuitive level without being exposed to it. They make small bets with terrible odds to stay in the game and improve odds for the next bet. Given the fact that serial founders have been playing the game for a while, their read and understanding of both odds and payoff is more accurate and effective than the crowd watching the game. What seems like reckless behavior to the world is actually an evolved response to years of effective risk taking. Only when odds begin to favor them do they increase the size of their bets. Founders use leverage when the conditions suggested by Thorp finally apply to them.
The house (status quo, incumbent players, vested interests) has an edge, but successful founders understand the game well enough to turn that edge to their advantage. They do this by hoarding capital till the odds and payoff favor them. To be fair this is not just Kelly. It is a model that mixes Kelly and optionality, but the point remains.
Optimal bet size is a function of odds. Even with the right odds, the optimal bet is a small fraction of your total wealth because you want to continue playing the game. An optimal strategy grows terminal wealth slowly over a finite investment horizon. It is not infinite. No one lives or trades forever.
Frameworks that require an infinite time horizon to outperform other frameworks need to be gauged with a finite lens where you put down your cards and walk away from the table.
Higher volatility in markets leads to higher risk and lower wealth. Think of volatility as a hazard rate or a utilization or capacity charge that eats into your capital balance. You need it to trade and build up your capital base because without risk there is no reward. Yet too much risk too soon or risk without adequate reward is likely to draw your capital balance down. Higher volatility may lead to higher potential payoffs but may also lead to higher losses and a bumpier ride to the end.
What is our takeaway?
There is no rushing into large payoffs. Large bets tend to be sub optimal. A sequence of smaller bets followed by well-timed large bets based on accurate estimation of odds and edges is likely to outperform a single large bet. Payoffs are a also a function of how long you can play the game or remain on the table. Some amount of patience is required and recommended. You don’t have to run a computational finance model on a supercomputer to follow this strategy. You can run the numbers on the back of an envelope when faced with your next sure thing. Survival, retaining your seat on the table and preservation of capital are the keys.
Kelly’s Criterion – The math
How does Kelly’s criterion work and what can we learn from it? What is the question Kelly equation trying to answer? In a game where you make one bet after another on odds that stay the same after each bet, is there a bet size that can optimize the rate of growth of wealth? Kelly answers this question with an optimal bet size given by the equation below:
f* = (bp – q)/b
where
f* = the optimal fractional bet size
p = probability of winning
q = probability of losing = (1-p)
b = edge is a function of payoff received for winners.
With an edge of 1.2 and even odds, the above formula gives us
f* = (1.2 x .5 – .5)/1.2 = (.6 – .5) / 1.2 = 0.0833
Which implies an optimal bet size of 8.33% of your bank roll for the wager described above.
There is an alternate and simplified presentation of fractional f* attributed to Merton which is:
f* = 2p -1
The same values above give us
f* = 2x(0.5) – 1 = 0% or an optimal bet size of 0 from Merton’s simplified model.
As per Merton a positive bet size should only occur when p is greater than q or when the probability of winning is greater than probability of not winning.
There is also another formulation for investing in equities attributed to Edward Thorpe. We won’t use it in this discussion but it’s a useful equation to know and it takes a while to dig it out.
f* = (m – r)/sigma^2
where
m = drift rate
r = risk free rate
sigma = standard deviation
References. Recommended reading.
Edward Thorp’s paper is what you need if you are thinking of applying Kelly to equity markets. Jamil Baz and Helen Guo do a terrific job of highlighting core issues with Kelly applications side by side with real world trading strategies. Ziemba response to Paul Samuelson challenges to Kelly is a great review of long term portfolio results of full and fractional Kelly investors. Finally four essays on Kelly by Philipp Winselmann also provide useful insights. From the point that Kelly caught my attention again in 2016, it took three years to get this simple four page article out. Which is surprising given how simple the underlying formula for optimal bet size is. Don’t be deceived by appearances or superficial analysis.
- The Kelly’s Criterion in Blackjack, sports betting and the stock market, Ed Thorp, 2007 – https://wayback.archive-it.org/all/20090320125959/http://www.edwardothorp.com/sitebuildercontent/sitebuilderfiles/KellyCriterion2007.pdf
- An Asset Allocation Primer: Connecting Markowitz, Kelly and Risk Parity, Jamil Baz and Helen Guo, PIMCO Quantitative Research, October 2017
- Response to Paul A Samuelson letters and papers on the Kelly Capital Growth Investment Strategy, William T Ziemba, November, 2012, https://www.him.uni-bonn.de/uploads/media/pas_or.pdf
- Essays on the Kelly’s Criterion and Growth Optimal Strategies, Kai Philipp Winselmann, PhD Thesis, January 2018
- Multiperiod Portfolio Optimization, Mark Broadie and Paul Glasserman, Columbia University, Security Pricing class notes, 1999
- https://demonetizedblog.com/2019/02/23/edge-over-odds/
- http://home.williampoundstone.net/Kelly.htm
- https://www.researchgate.net/profile/Ralph_Vince/publication/331111852_Expectation_and_Optimal_f_Expected_growth_with_and_without_reinvestment_for_discretely-distributed_outcomes_of_finite_length/links/5c663fee92851c48a9d4dfef/Expectation-and-Optimal-f-Expected-growth-with-and-without-reinvestment-for-discretely-distributed-outcomes-of-finite-length.pdf
- http://www.edwardothorp.com/wp-content/uploads/2016/11/TheKellyCriterionAndTheStockMarket.pdf
A chapter extract from Founder Puzzles, the brand new book that takes a different look on financial modeling for founders. Take a look

