Methodology
Setting the Scene
Sample Portfolio
Our sample portfolio that we will use for calculating Value at Risk (VaR) consists of the following 4 items:
- 100 shares of OGDC
- 5 barrels of Crude Oil
- 1 foreign exchange denominated asset with market value of USD 10 on 5th March 2010.
- 100 units of 3-year PIB with issue date of 19th February 2009 and coupon rate of 11.25%. This means that the outstanding term of the bond is 1.96 years.
Revaluation Date and Value of the Portfolio
We are calculating Portfolio Value at Risk (VaR) on the 5th of March 2010 at the end of the day.
Preliminary steps
The following steps are common to all the above mentioned Value at Risk (VaR) approaches:
Step P1: Determine look back period for Value at Risk
Determine the period over which the risk is to be evaluated. For illustration purposes let us assume a look back period of 5 days from 1st March 2010 to 5th March 2010. In practice window lengths cover a wider duration, such as 6 months, 1 year, etc.
Step P2: Obtain the daily times series data for each risk factor for the determined look back period for Value at Risk
The risk factors related to the assets in our portfolio are equity prices (OGDC), foreign exchange rates (USD-PKR), commodity prices (WTI) and interest rates (PKRV rates for 1 and 2 years respectively) as given below:
|
OGDC |
WTI* |
FX (USD-PKR) |
PKRV_1 year (%) |
PKRV_2 year (%) |
|
| 01/03/2010 |
116.51 |
6,695.01 |
85.0700 |
12.27 |
12.33 |
| 02/03/2010 |
117.32 |
6,781.38 |
85.1077 |
12.27 |
12.33 |
| 03/03/2010 |
116.40 |
6,877.91 |
85.0490 |
12.26 |
12.32 |
| 04/03/2010 |
116.58 |
6,812.55 |
84.9339 |
12.25 |
12.32 |
| 05/03/2010 |
117.61 |
6,911.20 |
84.8000 |
12.25 |
12.33 |
*WTI denominated in PKR = WTI denominated in USD×FX rate on that date. For example WTI spot price on 01/03/2010 was USD 78.70 per barrel. To convert this to PKR we multiplied this price with the FX rate for USD-PKR for that day, i.e. 78.70 × 85.0700 = PKR 6695.01.
Step P3: Adjustments to original time series data for Value at Risk
The interest rate risk factors, i.e. the PKRV rates, need to be adjusted to take into account the portfolio’s exact exposure to this risk factor. The PKRV rate series will first be interpolated based on the outstanding term to maturity of the bond and then will be converted into a price series which will be used in the actual VaR calculation:
The detailed steps to this process are given below:
- Determine the outstanding term of the bond. This is calculated as follows:
=1.96 years
- Calculate an interpolated PKRV rate series for this outstanding term. Interpolation will be done using the following formula:
T= outstanding term =1.96 years
T1=rounded down value of the outstanding term = 1 year
T2= T1+1 =2 years
Using PKRV rates for 5th March 2010, the interpolated rate is calculated as follows:
The resulting interpolated PKRV rate series works out to:
|
PKRV_interpolated (%) |
|
| 01/03/2010 |
12.3277 |
| 02/03/2010 |
12.3277 |
| 03/03/2010 |
12.3177 |
| 04/03/2010 |
12.3173 |
| 05/03/2010 |
12.3269 |
- Calculate the price of the bond at each data point using
- Settlement date = Revaluation date = 5th March 2010
- Maturity Date =19th March 2012
- Coupon Rate = 11.25%
- Yield = PKRV_interpolated (%) applicable to that data point
- Redemption value = 100
- Coupon payment frequency = 2
- Basis = Actual/365
This may be done using Excel’s Price formula or by discounting the cash flows using the following formula:
where:
t = number of days from settlement to next coupon date.
E = number of days in coupon period in which the settlement date falls.
N = number of coupons payable between settlement date and redemption date.
A = number of days from beginning of coupon period to settlement date.
The resulting bond price series works out to:
|
PIB Prices |
|
| 01/03/2010 |
98.1596 |
| 02/03/2010 |
98.1596 |
| 03/03/2010 |
98.1764 |
| 04/03/2010 |
98.1771 |
| 05/03/2010 |
98.1609 |
Step P4: Calculate a return series from the time series data for Value at Risk
A return series is derived from the given time series data by taking the natural logarithm of the ratio of successive prices/ rates, i.e.
where st is the price/ rate at time t. For example for OGDC the return on 5th March 2010
The return series for the rest of the portfolio is given below:
|
OGDC |
WTI |
FX |
PIB Prices |
|
|
02/03/2010 |
0.6928% |
1.2819% |
0.0443% |
0.0000% |
|
03/03/2010 |
-0.7873% |
1.4134% |
-0.0690% |
0.0171% |
|
04/03/2010 |
0.1545% |
-0.9549% |
-0.1354% |
0.0007% |
|
05/03/2010 |
0.8796% |
1.4377% |
-0.1578% |
-0.0164% |
Step P5: Calculate a return series for the portfolio
In order to evaluate the VaR for the portfolio, the return series for the portfolio will be required. This is derived by calculating a weighted average return series using the individual return series for each instrument in the portfolio. This will be calculated as follows:
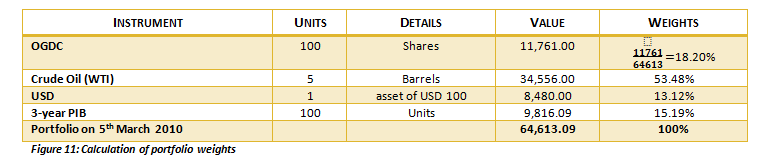
- Calculate the weights of the respective instruments in the portfolio on the revaluation date, where weight = value of the instrument÷total value of the portfolio. The weights for the portfolio are given below:
- Derive a weighted average return series by calculating for each point in time in the data series the sum product of the weight and return across instruments/ scrips in the portfolio. The resulting weighted average return series will be correlation adjusted, i.e. it will account for correlations between the various instruments. For example for data point 5th March 2010 the portfolio return will be
18.2%×0.8796%+53.48%×1.4377%+13.12%×(-0.1578%)+15.19%×(-0.0164%)=0.9058%.
The return series for the sample portfolio is as follows:
|
Portfolio |
|
|
02/03/2010 |
0.8175% |
|
03/03/2010 |
0.6062% |
|
04/03/2010 |
-0.5002% |
|
05/03/2010 |
0.9058% |
We can now move on to the next steps required to calculate Value at Risk (VaR)

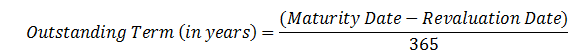
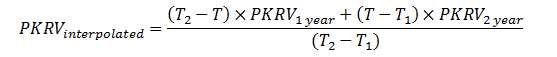

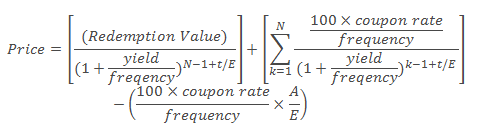

Comments are closed.