Earlier we had estimated the parameters of the Cox-Ingersoll-Ross (CIR) model from market data. We now apply these estimated parameters to the CIR Model process to simulate future short rates of interest. We will use the derived future short rates along with the implied perfect correlation between them and longer term rates to arrive at the complete term structure of interest rates.
Simulating future short term interest rates
Recall that the CIR Model process for the evolution of the short term interest rates was
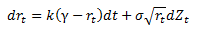
Where k represents the speed of adjustment (or mean reversion),
κ represents the long run mean of the short-term interest rate, and
σ represents the volatility
and dZt is a small random increment in the Wiener process zt having mean 0 and variance dt.
(Note: rt in this equation represents the actual interest rates and not the transformed rates as given in the calibration section above).
Using the estimation and calibration procedure above parameters k, γ and σ are derived. With these elements in place and using a time step, dt we are now able to simulate future interest rates by using the following equation:
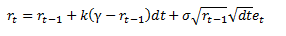
Where et are normally scaled random numbers generated in Excel using the function NORMSINV(RAND())
Modelling longer term rates
For a short rate one factor model like CIR the assumption is that there is only one source of randomness in the yield curve, which is the short term interest rate. This implies that longer term rates are perfectly correlated to the short term rate. Using this assumption is it then possible to model the longer term rates. Some methods of how this may be done is by assuming that the longer term rates change by the same proportion as the short term rates, another method is to assume that the current spreads between the short rate and longer term rate are representative of future spreads, etc.
This assumption of perfect correlation is one of the disadvantages of using the one-factor CIR Model as empirically this is not the case. Besides the level of the yield curve (as given by the uncertainty in the short rate) the yield curve may be impacted by other significant factors such as slope (or tilt as given by the difference between yields of different maturities), twist, etc.
In the post above we have looked at the simulation process for the short rate under the CIR model. In addition we have reviewed how we can apply the assumption of perfect correlation between short and longer term rates to derive the future term structure of interest rates. We have also assessed the disadvantages of making this assumption.
In the next posts we will be see how another one-factor model, the Black-Derman-Toy (BDT) model can be constructed in an Excel worksheet and how the results of that model may be utilized.
If you would like to buy this course as a PDF file or the sample EXCEL sheets, please see the Interest Rate Modelling section at our online finance course store.

Comments are closed.