In this post, we explore CIR Model parameter estimation. In other words, we consider how to calibrate the Cox Ingersoll Ross interest rate model to real world data.
The existing literature contains a number of papers that seek to estimate the parameters of the short rate models. Different authors use different data sets, time periods, sampling frequencies, and empirical methodologies.
The empirical methodology we have considered for CIR model parameter estimation is the LSE (Least Square Estimate). Various researches on the subject have revealed that the parameter estimates are sensitive to the choice of empirical methodology.
When using discrete data for estimating the parameters of a continuous model, one needs a discrete representation of the process. We will consider two representations below.
The first is a simple discretisation process with function:
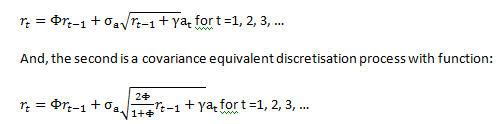
Under both processes, the principle involved is that the first two moments of both the discrete and the continuous models should be equal.
CIR Model Parameter Estimation Process
The process is as follows:
1. Obtain the interest rate series (rt*) for the given benchmark yield curve (e.g. for 3-month rates).
2. Determine a centered CIR model. Subtract the rates at each data point with their long run average (γ) across the entire series to obtain a transformed series (rt).
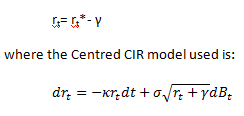
3. Use the least squares method is to estimate the parameters for the discrete representation of the CIR model. We do this as follows:
a. At each data point calculate the following residual term:


We have considered the least squared method of estimating parameters for the continuous CIR model using two discretisation techniques; Simple Discretization and Covariance Equivalent Discretization. The next post will look at how to use these estimated parameters in the model to simulate future short rates and consequently the term structure of interest rates.
References:
- A covariance equivalent discretisation of the CIR model – Deelstra & Parker
- The Volatility of Short-Term Interest Rates: An Empirical Comparision of Alternative Models of the Term Structure of Interest rates – K. C. Chan, G. Andrew Karolyi, Francis A. Longstaff and Anthony B. Sanders

Comments are closed.