We review the one-factor equilibrium Cox Ingersoll Ross (CIR) model and its primary features.
The short-term interest rate is one of the key financial variables in any economy. It is a target instrument that central banks use to implement monetary policy and an important economic indicator for regulators and governments. It is also a key variable for business since it forms the basis of floating rate loans and most of the financial instruments that can be used to manage interest rate risk. Moreover, longer-term interest rates reflect, at least in part, the expected values of future short rates. The short rate is also a relevant input in determining the required return on any asset. For all of these reasons, a good model of the short-term interest rate is of great practical importance.
Most of the popular short rate models incorporate two key features: mean reversion and non-constant volatility. In particular, most models allow for the short rate to revert to a long-run mean so that if the current rate is above (below) the long-run mean it is expected to decrease (increase) towards the long-run mean in the future. The volatility of interest rates is often made to be dependent on the level of interest rates so that when rates are higher, they are more volatile.
The CIR Model (1985) is a one factor equilibrium model. It is linear mean reversion model and uses a diffusion process different than other short rate models. The short rate in a CIR model follows a square root diffusion process which ensures that the short term interest rates are always non-negative. The process follows the continuous-time representation given below:
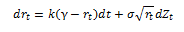
where k represents the speed of adjustment (or mean reversion),
gamma represents the long run mean of the short-term interest rate, and
sigma represents the volatility
and dZt is a small random increment in the Wiener process zt having mean 0 and variance dt.
Under this model, both the drift and the volatility change with the level of the short rate. The stochastic term has a standard deviation proportional to the square root of the current short rate. This implies that as the short rate increases, its standard deviation increases. As mentioned earlier this also means that the short rate under the CIR model will be strictly non-negative. As the short rate falls and approaches zero, the diffusion term (which contains the square root of the short rate) also approaches zero. In this case, the mean-reverting drift term dominates the diffusion term and pulls the short rate back towards its long-run mean. This prevents the short rate from falling below zero.
We have reviewed the CIR model, in particular its short rate mean reversion feature and the square root diffusion process. In the next post we will look at how the parameters of the CIR model are estimated and how the model is calibrated to historical data. Please see Calibrating CIR parameters, simulating interest rates in Excel.
For sample CIR EXCEL sheets and a more detailed PDF writeup, please see the Interest Rate Modelling section at our online finance course store.

Comments are closed.