Bond Convexity calculation example
A working example of bond convexity and sensitivity calculation. Earlier we had reviewed the calculation process for Effective Duration. In this post we will see how bond convexity is calculated. We will also see how the Effective Duration and Convexity are brought together to estimate the % change in price brought about by a % change in yields, in other words, the sensitivity of the sample fixed income instrument to interest rate changes.
Effective Convexity
Effective Convexity is calculated using the following formula:
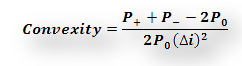
Effective Convexity = (97.2691+99.0768-2*98.1666)/(2*98.1666*1%^2) = 0.6461
Sensitivity
Using Effective Duration and Convexity, it is possible to estimate by how much the price of the instrument will change in response to a change in yield rates. The estimate of the % change in price is given by the following formula:
Total estimated percentage price change= -Duration× change in i×100+Convexity×(change in i)2×100
So for a 1% decrease in the yield rates the total estimated percentage price change is:
-.9208 * (-1%) * 100 + 0.6461 *(- 1%)^2*100 = 0.9272%
This means that a 1% decline in yield rates will result in a 0.9272% increase in price.
Applying this to the initial price (P0) we see that a 1% decline in yield rates will cause prices to rise from 98.1666 to 99.0768 [= 98.1666*(1+.9272%)]. This as we can see from the calculation of P- above is equal to the actual price when the yield decreased from 12% to 11%.
In this post we have seen how Effective Convexity has been calculated. We have also seen how the Effective Duration and Convexity metrics are used to estimate the % change in price of an interest rate sensitive instrument when yield rates changed. If you are interested in practical application of duration and convexity in Asset Liability Management reporting and systems also see ALM for Board Members – 7 lessons in 60 minutes.

Comments are closed.