Option Greeks – Theta
This article is closely based on the paper “A closer look at Black–Scholes option thetas – Douglas R. Emery &Weiyu Guo & Tie Su, October 2007″. We use the framework presented in the research paper to look at Theta for European Call options from a slightly different perspective.
Consider the following at the money European Call option on a non dividend paying stock:
Call option theta is calculated as follows:
Theta relative to underlying asset value, S
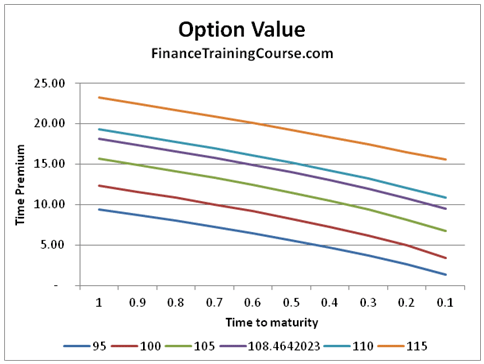
The following graph shows the value of the option at varying times to maturity. Each line represents the value overtime for a different underlying asset value S.
In general as the option approaches maturity the value of the option declines.
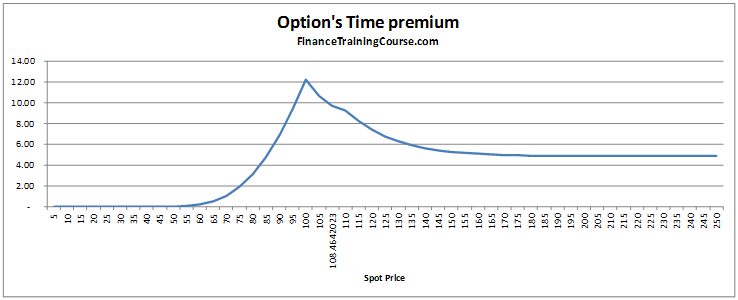
The option’s time premium is greatest when S=X as shown in the following graph. Keeping all other parameters/ assumptions constant, the time premium represents the change in the value of the option as the option approaches expiration. It is calculated as the difference between the value of the option at inception and its value at expiry:
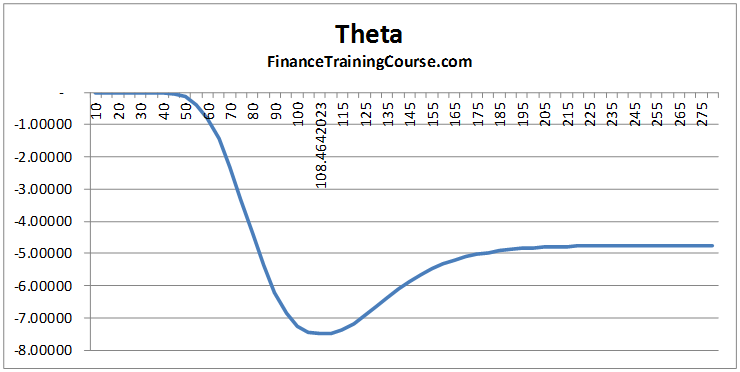
The rate at which this time premium dissipates for different values of S is given in the following graph which plots option thetas on the y-axis against the underlying asset value on the x-axis:
The graph shows the sensitivity of theta for the option to various spot prices. It indicates the rate at which the value of the option’s time premium declines overtime. For a call option the theta is always negative which means that the value of the option’s time premium will always dissipate as the options approaches maturity. For deep out of the money options there is no dissipation in the time premium. As the underlying asset value approaches the strike price the rate of dissipation increases. When the option is in the money, the rate of decay falls and then levels out for deep in the money options.
As S approaches positive infinity, i.e. the option is deep, deep in the money, theta approaches the value:
Risk free rate * Strike * exp(-Risk free rate * Time to expiry)
For the given option this value is -4.75615.
As S approaches 0, i.e. the option is deep out of the money, and theta approaches the value of zero.
The maximum rate of dissipation is reached around the point where the option is at- the-money, more specifically when the spot price is slightly greater than the strike price, i.e. when:
S = Strike*exp(Risk free rate * time to maturity + (Vol^2)*time to maturity/2)
For this instance the maximum value of theta is reached when S = 108.4642 as seen in the graph above and more clearly in the table given below:
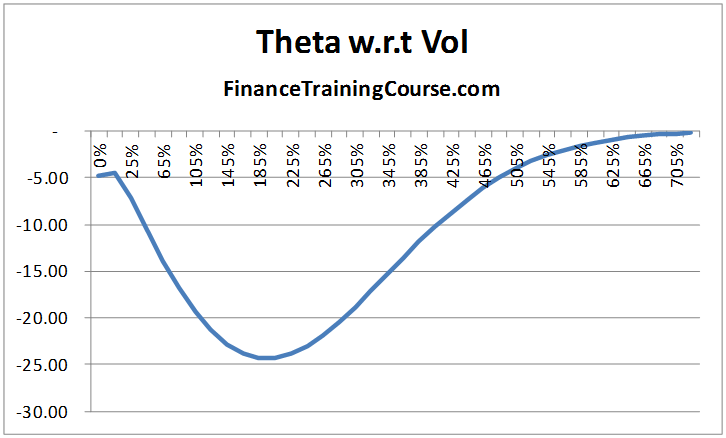
Theta relative to volatility
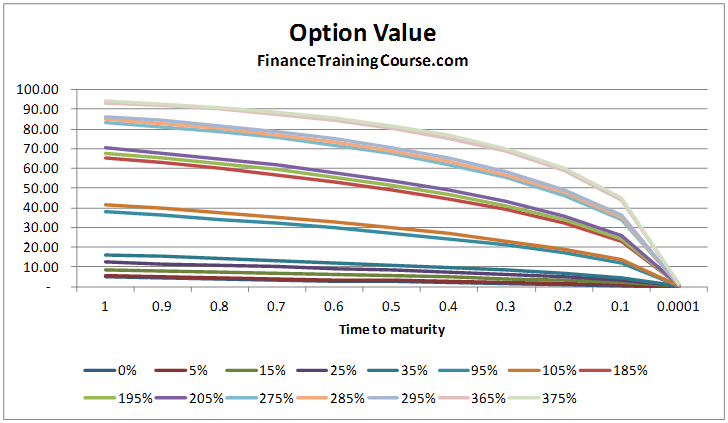
The option’s time premium is an increasing function of volatility. As volatility increases the value of the option increases:
While the option value declines overtime regardless of the level of volatility:
the rate at which the time premium declines overtime depends on the level of asset return volatility. It is not a monotonic (i.e. only increasing or only decreasing) function in return volatility:
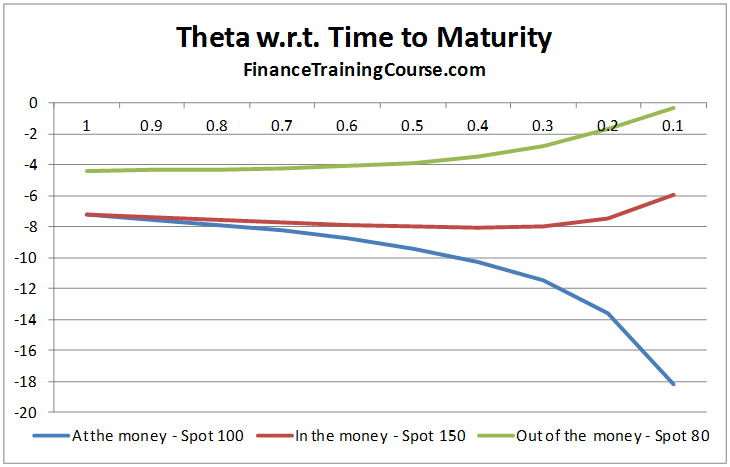
Theta relative to time to maturity
As already seen above the option value declines as the option approaches maturity however depending on the money-ness of the option the theta many be increasing or a decreasing function of time:
For in and out of the money options the rate at which the option’s time premium declines remaining fairly constant over the life of the option and then decreases as the option approaches expiry. For at the money options the rate of decay is much higher increasing as the option approaches maturity.
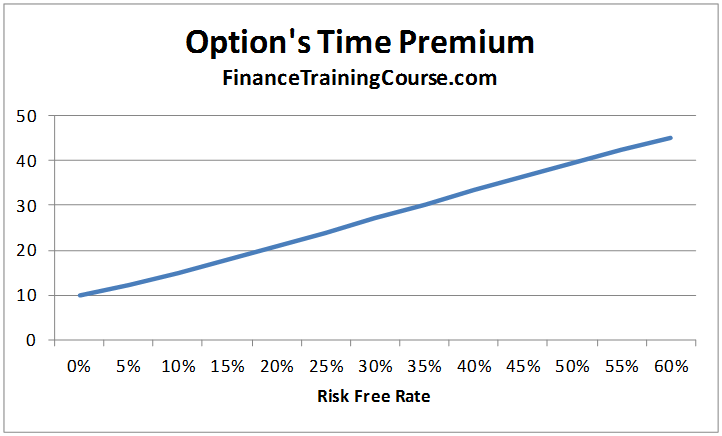
Theta relative to the risk free rate
The option’s time premium increases as the risk free rate increases:
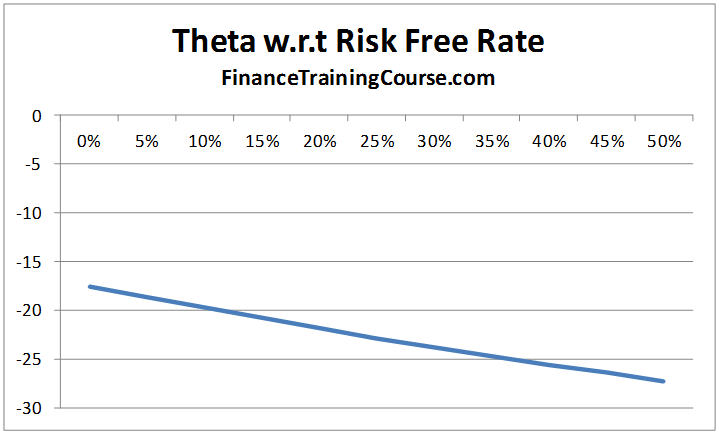
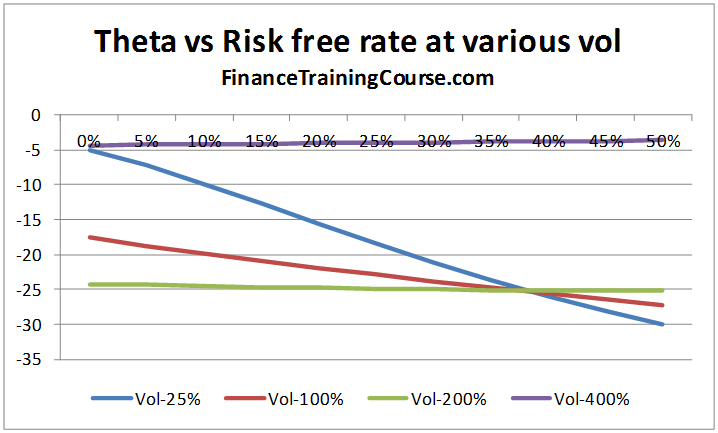
At first glance the option theta’s also appears to be a monotonically decreasing function of the risk free rate, declining as the risk free rate increases, i.e. as the risk free rate increases the rate of decay of the options time premium increases:
However at extreme values of return volatility, the rate of dissipation tends to reduce when the risk free rate increases (see the purple line for volatility of 400% below):
References:
- A closer look at Black–Scholes option thetas – Douglas R. Emery &Weiyu Guo & Tie Su, Oct 2007
- Options, Futures and other Derivatives – John C Hull, 7th Edition