Option Greeks – Building the Solver model for hedging Greeks
Our first attempt to hedge higher order Greeks is a simple illustrative scenario with a single option contract. We start off where we stopped in lesson one on hedging higher order Greeks.
We have sold (written) a single position in a call option on NVIDIA (NVDA) on 14th May 2014. Our objective is to hedge Gamma and Vega exposure using a universe of cheaper options on the same date. Our model will essentially look for an optimal combination of cheaper options that completely or partially offset our Gamma and Vega exposure. Since we have sold (written) options we are short Gamma and Vega. Our offsetting position requires a trade that will be positive Gamma and Vega. The positive Gamma and Vega trade is possible when we buy options or pay the premium.
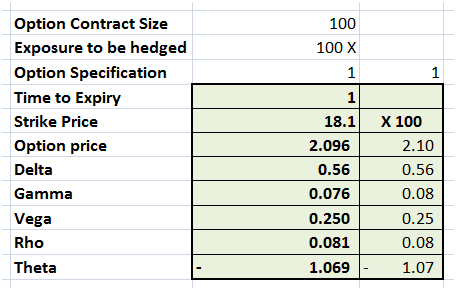
Here is the original option specification for the call option contract that has been written by our desk. Each contract that we write includes a bundle of 100 options. In our initial model and trial run we will solve for a single option and then scale the results for 100 contracts.
Figure 1 Hedging Greeks – Our short position
Of the above specification the two things of immediate interest to us are the option premium ($2.1) and the expiry (1 year). Our hedge portfolio cannot cost more than $2.1 and while we can play with the expiry of our hedge portfolio we would ideally like to match it as much as possible with our short exposure.
Gamma and Vega exposures – Positive or negative?
Should you leave some residual Gamma and Vega exposure or should our hedging portfolio neutralize it in its entirety? From the fixed income and ALM world comes an interesting parallel. In the ALM world to preserve surplus or immunize capital from interest rate changes we match the weighted average of the first order sensitivity (modified duration) but we require that the second order sensitivity (convexity) of Assets is great than the convexity of liabilities.
Similarly in the options world while we may match Delta completely, we would aim to create a hedging portfolio with excess Gamma and Vega exposure compared to our original short position. If that is not possible we will let the positions run with the Gamma and Vega mismatch but use exposure limits to track our sensitivity to these two factors. Our hedge is going to be an imperfect semi-hedge which would leave some room for benefiting from unanticipated changes in market volatility as well as large unexpected jumps in the price of the underlying.
Hedging Higher Order Greeks – Structuring the problem.
The first question that comes up for discussion is that within the settings of Excel solver what objective function will we use to create our semi-perfect hedge. The objective function is the cell Solver will optimize. Since it is a single cell and we have two targets (Gamma and Vega exposure) we would need to be creative to structure a variable that will lead to exposure minimization under both the heads.
The second question revolves around the constraints we need to define an acceptable solution. We address both in this section.
Model design.
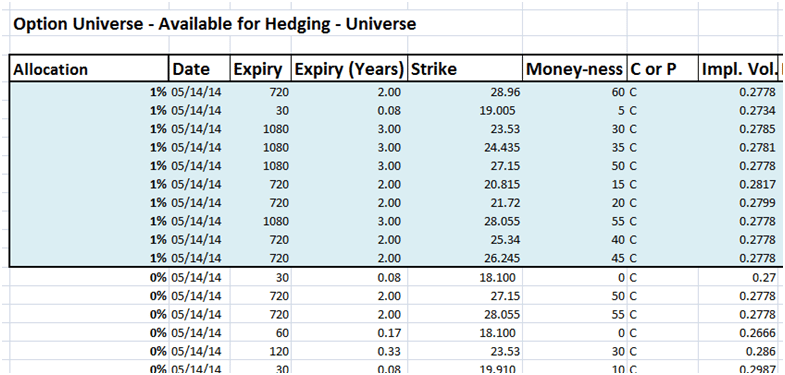
Our first step is to put aside the universe of options available for hedging. For our first round we limit the universe to call options. On 14th May 2014, there were around 104 call options that were available across the combination of maturities and strikes. The universe excludes 10 longer maturity options that we have selected for short positions.
We add a new column at the beginning of the universe titled “Allocation” which we will use in our solver model to allocate hedge portfolio weight to a given option contract.
Figure 2 Option Hedging Universe – The selection of options available to hedge Gamma and Vega
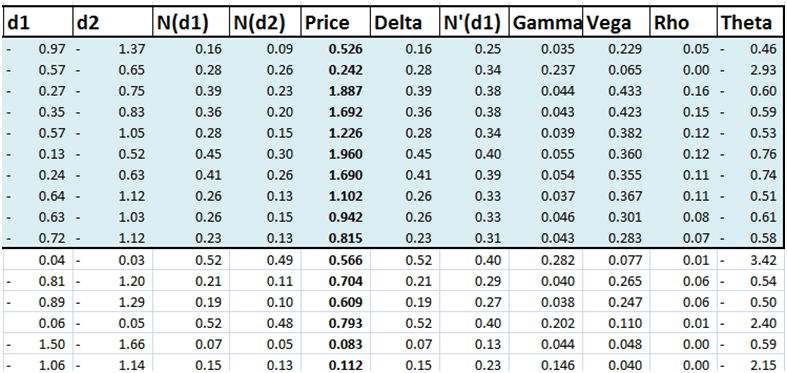
We have already calculated Greeks in lesson one. We now add values for Greeks against each option in the hedge universe.
Figure 3 Adding Greeks to the Options Universe
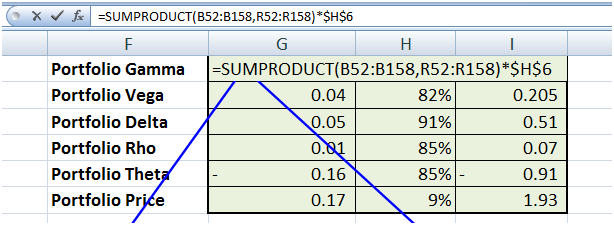
Option Greeks are then used to calculate our hedge portfolio Greeks. For each of the Greeks in the table below the formula is a simple sumproduct of the hedge portfolio allocation weight and the Greeks in question. The first vector in the formula below is the portfolio allocation weight, the second is the Greek in question across the universe. The multiplier is the scaling factor that we will use later to scale results from 1 option contract to 100 contracts.
Figure 4 Calculating Hedge portfolio metrics
Applying this formula for each of the Greeks give us the following table of hedge portfolio Greeks. We will use elements of this table in our model.
Figure 5 Hedging portfolio metrics
We have most of the components we need to setup the Solver model.
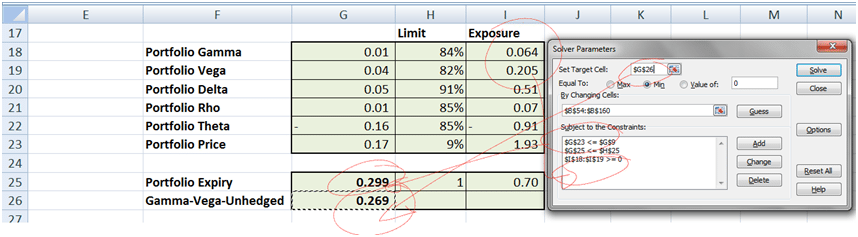
For our objective function we create a new cell titled Gamma-Vega-Unhedged which is the simple sum of Gamma Vega un-hedged exposure from the table above. Our first iteration solver model will aim to minimize this number. To ensure that we don’t run into negative territory we will assume a non-negative model.
Figure 6 Solver objective function
In terms of constraints the first constraint we want to setup is to ensure that our average hedge portfolio expiry is less than the short position maturity. A second constraint would be to ensure that the hedge portfolio Gamma and Vega figures are atleast the same but ideally greater than the Gamma, Vega estimates for our short position.
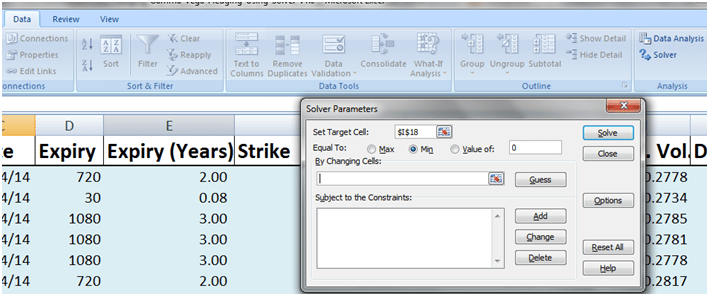
Let go ahead and set up the model. To use the solver add-in click on the Data tab in Excel and chose the Solver add-in. If you don’t see the Solver add-in please use the Excel setting to enable the add-in. The add-in is only available in the professional edition of Microsoft Office/Excel.
Figure 7 Solver screen at step zero
You now have the required blank slate.
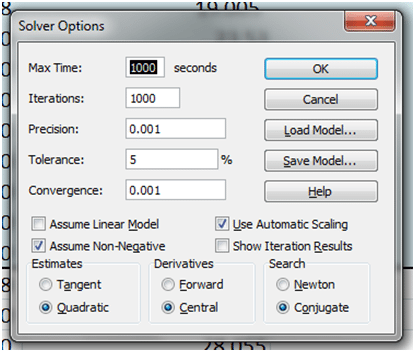
Step 4 is to configure Solver options to ensure non-negative values. In addition to the non-negative values we also want to use a quadratic model for estimates and conjugate method for searching optimal solutions.
Figure 8 Setting Solver parameters
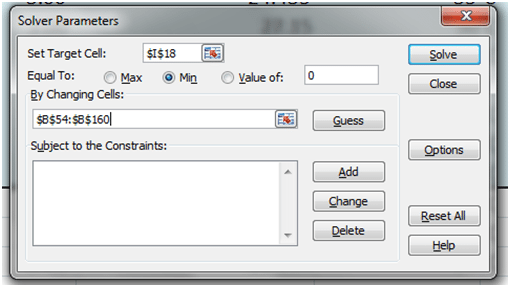
Step 2 is to setup the objective function cell. This is the Gamma-Vega-Unhedged cell.
Step 3 is to identify the cells Solver will change. This is range of cells under the portfolio allocation weight under the Allocation column.
Once you are done with both steps, the Solver model will look like:
Figure 9 Defining portfolio allocation
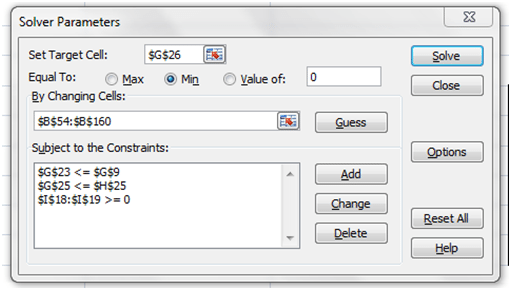
Step 4 is to define the constraints with respect to expiry and premium discussed above. Which we do below.
Figure 10 Adding constraints
Here is how the objective function and two of the constraints link up with the relevant cells.
Figure 11 Bringing it together
Note that there are a number of additional constraints on the number of option contracts the hedge portfolio can include (how many?) as well as the proportion of the original premium available for hedging that we haven’t defined. What we would like to do is to try and run this model with these bare minimal conditions and see what kind of a solution Solver throws up and then refine and fine tune the model by adding additional constraints.
If you want to give it a shot, go ahead and press solve to run solver on your newly built Gamma and Vega hedging optimizer model. Before you press Solve make sure that you save your work. What does your solution look like? What is the recommended allocation and cost?
We review the results and the tweaks in our next post on hedging higher order Greeks tomorrow.



Comments are closed.