The prerequisite for this course is the first course on pricing interest rate swaps.
And the second more advanced course on interest caps, interest rate floors and other related fixed income options. The same foundations defined here can be used to price range accrual notes as well as commodity linked notes as described in the next two concepts
- Online Finance – Pricing a Cross Currency Swap – Floating for Floating structure
- Online Finance – Pricing a Cross Currency Swap – Amortizing and Indexed Term sheets
- Online Finance – Interest Rate Options – Pricing Caps & Floors
Range Accrual Notes
Range accruals are a form of interest accrual in which the payment is only earned on days when a specified benchmark rate falls within a specified range.
As the payment is conditional on the rate following within a certain range, the cash flow is multiplied by the probability of such an event occurring. The probability is calculated as the probability that the rate will exceed the lower boundless the probability of it exceeding the upper bound of the range.
The probability that the rate, Fi, will exceed a given rate, X, is given by N(d2) where

N(.) is the cumulative standard normal distribution and ? is the volatility of Fi.
To illustrate, we have the following term sheet for a range accrual note:
| Item | Terms and Conditions |
| Notional | 100,000 |
| Binary Rate | 12.00% |
| Payment | Annual |
| Payment Dates | 1st Day of the year starting January 2011 and ending on the Maturity Date |
| Valuation Date | 01/06/2010 |
| Maturity Date | 01/01/2014 |
| Day count convention | A/365 |
| Lower Bound | 12.00% |
| Upper Bound | 12.20% |
| sigma (volatility of Fi) | 4.00% |
The instrument pays 12% annually if the benchmark rate falls with the range of (12%, 12.2%).
The results will be as follows:
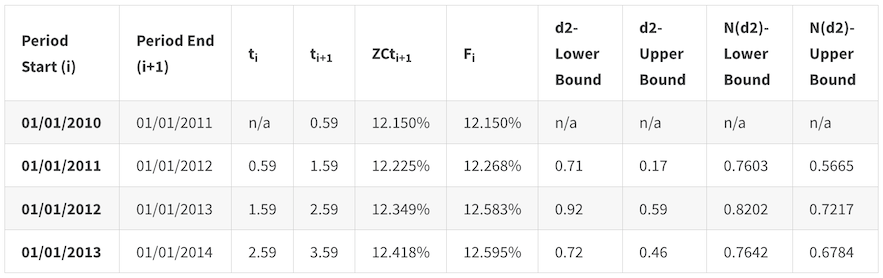
‘d2-Lower Bound’ uses the Lower Bound rate of 12.00%, as X in the formula, whereas ‘d2-Upper Bound’ used the Upper Bound rate of 12.20% as X in the formula. In the first row, the d2 values are “n/a” because the period start date falls before the valuation date.
The probability that the rate will fall within the range is equal to ‘N(d2)-Lower Bound’ minus ‘N(d2)-Upper Bound’. For the first row the probability will be 1 if Fi lies within the range and 0 otherwise.
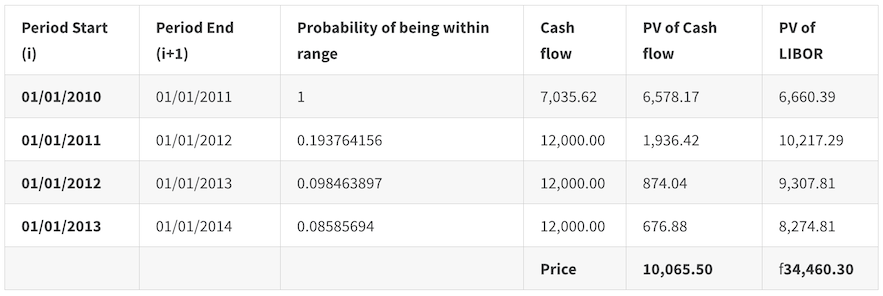
The Cash flow column is equal to the Binary Rate (i.e. the rate at which payments are to be made) * Notional. For the first period, since it is fractional, the cash flow will be multiplied by the remaining tenor in that period to determine the payment, i.e. 12%*100,000*0.59.
The PV of Cash flow = (Cash flow*Probability) / ((1+zcti+1) ^ ti+1 ).
For comparison purposes we show the present value of the actual LIBOR payment = (Fi *Notional)/( (1+zcti+1)^ ti+1 ). Again for the first period, the payment is adjusted for the fractional period.
The price is the sum across PVs.
For a complete reference to equations and calculator referred to in our course catalog, please see the Derivative Pricing and Financial Risk Equation Glossary.
For topic specific equations, please see the following links:
- Calculating Value at Risk
- Duration, Convexity and Asset Liability Management
- Black Scholes, Derivative Pricing, Binomial Trees
- Calculating Forward Prices and Forward Rates
- Valuation of Interest Rate Swaps and Future Contracts
- Financial Risk, Reward metrics and measures
- Black Formula’s, Valuing Interest Rate Caps and Floors

Comments are closed.