And now for the last and final part of our Practice Exam Test Question series on how to price & MTM IRS (Interest Rate Swaps). In our first post, we walked through the process of building an annualized forward curve and then extending it to semiannual rates. In this post, we will take the forward curve generated in the previous post and use it answer our Interest Rate Swaps (swap rate) and mark to market (valuation) questions.
The projected zero and forward rates curve from our previous post is posted here for convenience. Before you proceed further please take a quick look at the interest rate swap pricing free study guide to review our approach and methodology.

Price & MTM IRS – Partial Solution
Here is the output from our solution Excel Sheet. The approach is as per interest rate swap pricing free study guide. The projected forward rates were derived in the projected forward rates using bootstrapping post. As you can see that the trick here was recognizing that we didn’t have a normal interest rate swap but a forward starting amortizing swap and then adjust the pricing approach accordingly.
a) The exact breakeven swap rate is 13.718% and the breakeven value of each leg (fixed and floating) is 3.001609 million.
b) Since the client is hedging a floating rate loan with this swap he will be paying a fixed rate and receiving the floating rate or simply paying fixed.
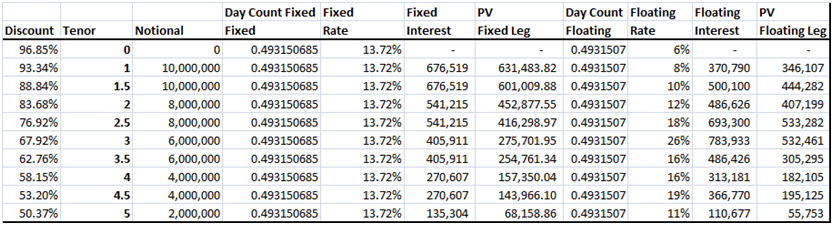
c) This question is asking you to price a one step FRA or a Forward Rate Agreement. To solve it, pick the row corresponding to tenor 2.5. Solve for a fixed rate that allows the present value of fixed and floating payments to completely offset each other. This fixed rate is 17.5732%. Intuitively, without resorting to the solution below, the breakeven rate is equal to the applicable forward rate.

Common Interest Rate Swap pricing and valuation mistakes made by students in this question
- Not making the forward pricing adjustment for the forward starting interest rate swap
- Not using the correct notional amount. Some students used a flat value of 400 million rather than the amortization schedule shared with the question above. Use the correct amortization schedule
- Not adjusting for the day count in the fixed as well as floating cash flows. Students often use the full rate when calculating the semiannual payment. Instead, they should use 180/360 or 182/365 * the relevant interest to account for a semiannual interest payment.
- Not using the correct applicable floating (forward rate)
The pricing of the interest rate swap six months later after the interest rates term structure change
We assume the original Swap structure and that it was purchased at the original breakeven Swap rate

The answer to this question requires a simple re-application of the above process one more time. Here are the revised projected forward rates

The trick is to remember that we have moved 6 months forward in time and the IRS is effective now. Based on this assumption this is how the revised grid looks like. The IRS has a negative MTM of -1,575,684 because we had expected rates to go up and they have actually come down.

Once again the biggest mistake students made here was not moving forward in time and pricing the IRS on an as is basis. The second biggest mistake was not using the updated curve and the old Swap Rate calculated from the earlier part of the question.


Comments are closed.