Since a spot, forward or future position is linear in its pay off it has no second order derivative. Options on the other hand are non-linear (asymmetric payoffs). While we can get away with hedging Delta with a linear position because Delta is a linear approximation (a tangent used to estimate the rate of change) we cannot hedge higher order Greeks (such as Gamma) exposure by buying a position in the underlying.
Vega brings additional challenges. We don’t directly observe volatility and the impact of changes in volatility are not linear and cannot be modeled or hedged using linear instruments. They vary based on money-ness and the time to maturity of the option.
To hedge these non-linear changes represented by Gamma and Vega we have to try a non-linear recipe. We have to buy similar (ideally cheaper) options.
In this chapter we start with building a simple Excel spreadsheet that will us allow us to hedge Gamma and Vega exposure for a single short position in a call option contract. The Gamma and Vega hedge would be created by buying cheaper out of money options with shorter or similar maturities than the original exposure.
For our first example we will build a simplistic spreadsheet focusing more on learning to work within the hedging domain using Solver in Excel. We will hedge a single position with a portfolio of cheaper options but our optimization metrics and our solver constraints would be simplistic.
Our second example would try and hedge a portfolio of short positions in options with the same universe of cheaper options used in the first example. But we will add new optimization metrics and solution constraints that would bring the model closer to practice. Please note that both examples are contrived to illustrate specific modeling points. The actual hedging practice will vary from desk to desk and from one market to the next.
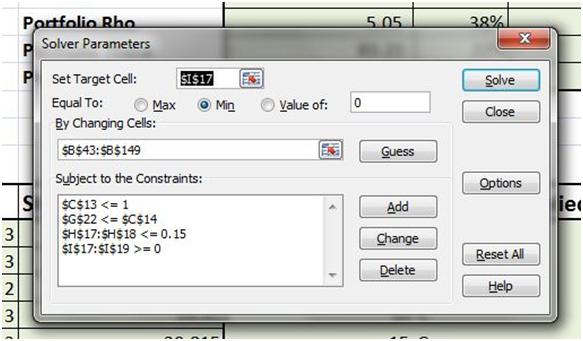
Figure 1 Hedging higher order Greeks. Using solver to create a hedging portfolio for Gamma and Vega exposures
Hedging higher order Greeks for a single short position
Here is the step by step approach that we are going to use in building our Solver spreadsheet for hedging higher order Greeks. Let’s look at each of these steps.
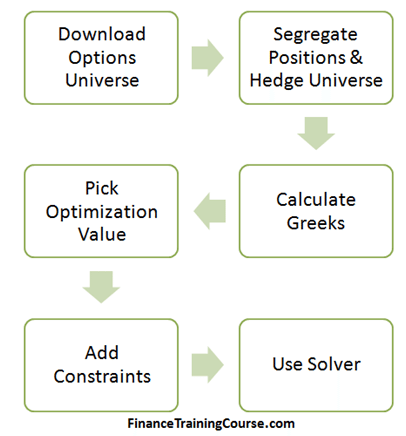
Figure 2 Hedging higher order Greeks. Required steps
Options Universe Dataset
For the date on which the hedge will be put in place we need the entire universe of available options on that date with the implied volatility data. For ease of use we sort the options universe by expiry and this becomes our raw data set. We will now refer to this as the universe.
We segregate the universe between the options we are going to sell and the options we will use to hedge our short positions within the spreadsheet. There are 13 at the money or near money options that we select for selling. There are 104 that will serve as our universe of hedging instruments.
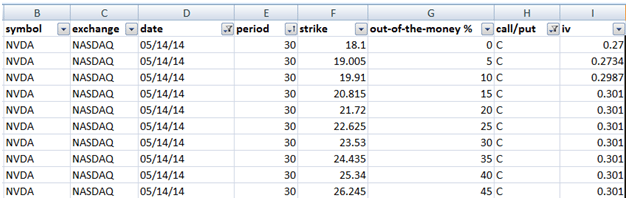
Figure 3 The default options universe
Our next step is to calculate Greeks for the entire universe. Which is what we have done in our next panel.

Figure 4 Calculating delta
We now need to determine the appropriate optimization value and the associated constraints for our solver model. We cover that in our series of next lessons. Stay tuned.

Comments are closed.