Hedging Higher order Greeks – Lesson Three
We are now ready to solve the Gamma Vega hedging optimization model in Excel created in our first two lessons earlier. For a quick review see:
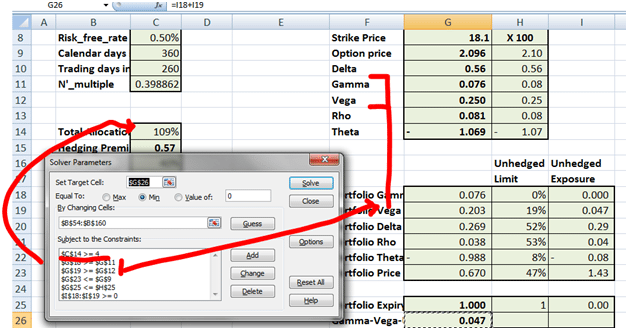
When we press the solve button on the Excel Solver add-in what does the solution recommended by Solver looks like?
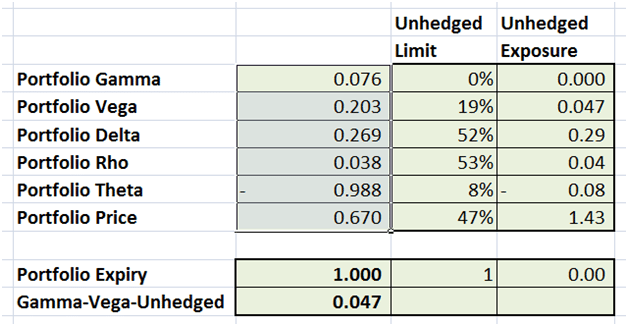
Figure 1 The Higher Order Greeks Hedging solution – First pass
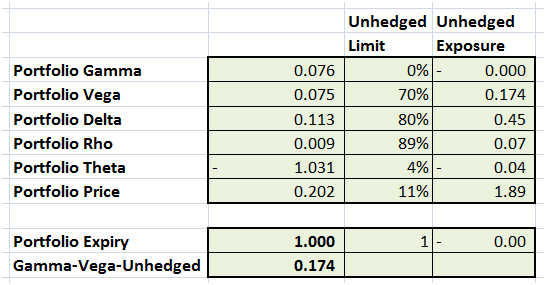
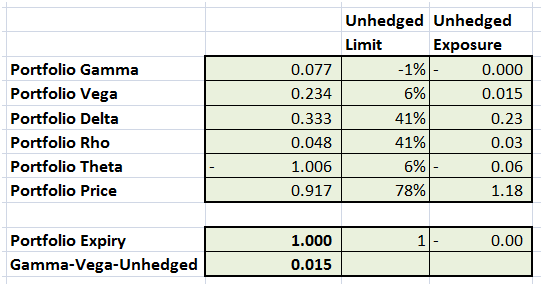
You can see that the Gamma Vega objective function has been minimized to .047%. Within that minimization, Gamma has been completely neutralized while there is some residual Vega exposure left. While we didn’t focus on the minor Greeks (Delta, Rho, Theta) these exposures have also been reduced.
How does it compare to the original short position? Let’s take a quick look
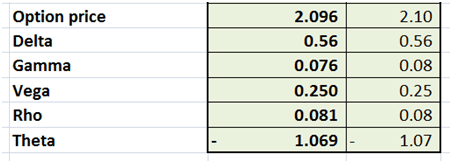
Figure 2 Comparing the two sets of Greeks. The Hedge versus the short position
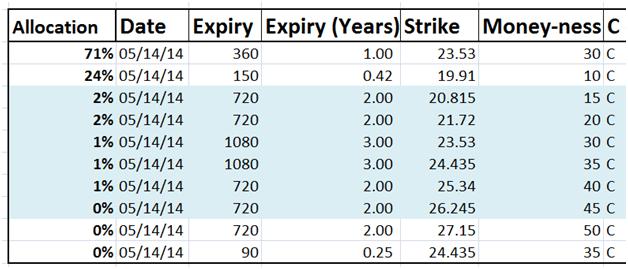
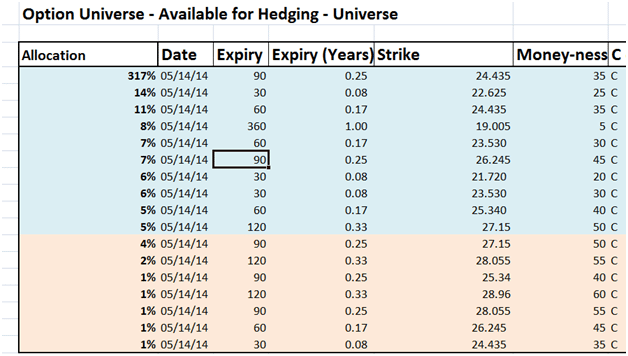
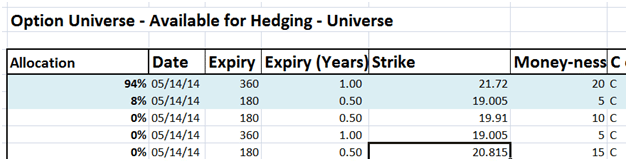
What instruments were picked and recommended by the solver solution? The solution picked 2 major positions and 5 minor positions. The majors were out of money options with expiries within a year. The minors were all deep out of money options with longer dated expiries.
Figure 3 Hedge portfolio – First pass
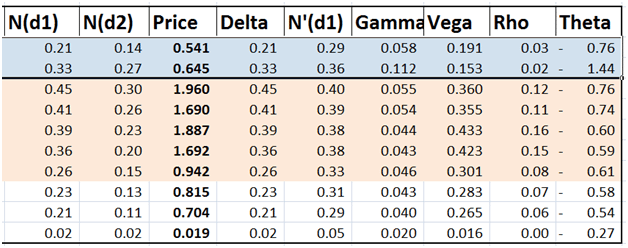
Why? Let’s take a look at their Greeks to understand the logic behind these recommendations. The model is essentially calculating the cheapest Gamma to premium ratio while focusing on the constraints it has been asked to solve. The Vega solution is possibly more intricate so Solver focuses on solving what it can solve. We will tweak our model later in the post to see if we can get a better Vega resolution than the current solution.
Figure 4 Hedge portfolio Greeks – First pass
Is there a better solution possible?
Let go ahead and add three new conditions.
1. Hedge portfolio Gamma and Vega should be greater than short position.
2. To ensure that this happens we force the model to buy multiple options. This is a condition that didn’t exist before. Now the model can buy multiple option positions rather than limiting ourselves to just 100% allocation. In the next two solutions you will see the impact forcing this condition makes on the structure of the recommended solution as well as the total cost of hedging.
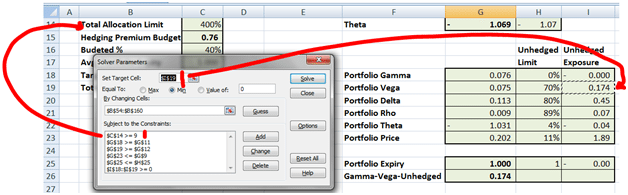
Here is what the revised solver model looks like:
Figure 5 Tweaking the Solver Hedging model
How do these new conditions change the solution? Solver fails to find a perfect solution but at the point it gives up we have a partial solution that we can review.
Figure 6 Hedging higher order Greeks – Second pass
What does the universe of recommended solutions look like now?
Figure 7 Hedging solution – forcing a deep out of money solution
The original solutions recommendations have changed dramatically. We now have 10 major and 7 minor positions. Unlike our earlier solution in this instance they are all under one year maturity and they all are deep out of money options.
What if rather than focusing on Gamma and Vega we only focus on our attention on Vega? What would that do to our recommended hedges.
Here is the revised Solver model. Note that the objective function now focuses only on minimizing the Vega difference between the hedge portfolio and the original short position. We have also jacked up the allocation force to 900%.
Figure 8 Hedging higher order Greeks – Third & fourth pass
What does the solution look like now? Solver fails to find a solution so we go ahead and change two of the conditions above from our Solver model. We drop the multiple position force and we remove an additional Vega limit condition that may confuse Solver. Under the revised set of conditions Solver immediately finds a solution.
Figure 9 Minimizing Gamma and Vega exposure
Despite the fact that Gamma is no longer part of the objective function, we still have a solution that minimizes both Gamma and Vega un-hedged exposures. The cost of the hedging portfolio however has gone up.
What instruments are recommended and used by Solver? Positions are down to two with shorter maturities. You can now see why the multiple position force was added as a condition. It pushes Solver to focus on deep out of money options and it allows us to keep the hedging cost to a minimum.
Figure 10 Hedging higher order Greeks – Final solution.

Comments are closed.