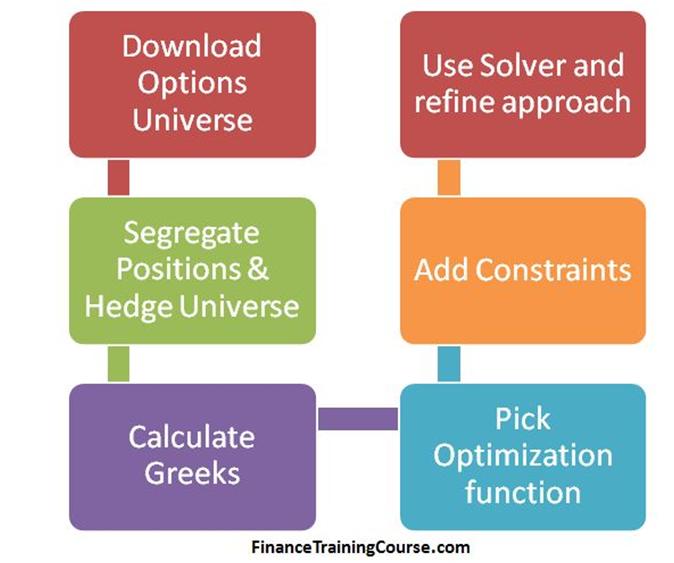
We build a simple Excel spreadsheet that allows us to hedge Gamma and Vega exposure for a single short position in a call option contract. Gamma and Vega hedges are created by buying cheaper out of money options with shorter or similar maturities.
The five lessons that follow review the methodology used to build the hedging sheet in Excel.
For our first example, we will build a spreadsheet focusing more on learning to work within the hedging domain using Solver in Excel. While we hedge a single position with a portfolio of cheaper options but our optimization metrics and our solver constraints remain simplistic.
Our second example extends the same framework for a portfolio of short positions by adding additional optimization metrics and new constraints.
1. Lesson One – Hedging Gamma and Vega – Introduction
Introducing the framework used to build the Excel model for hedging higher order Greeks.
2. Lesson Two – Hedging Gamma and Vega – Building the Solver Model
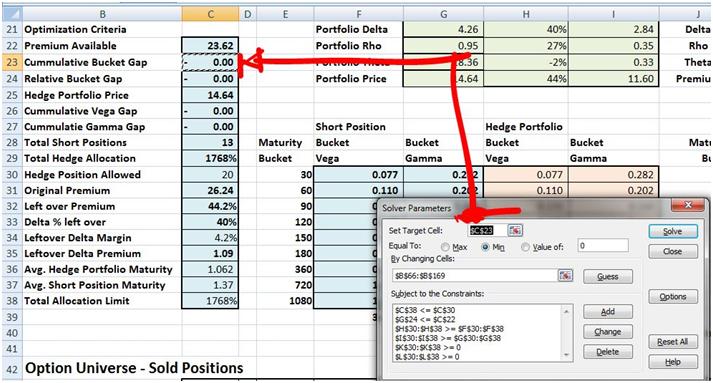
We begin with a simple single position Solver model that hedges higher order Greeks (Gamma and Vega) using a universe of available out of money options using a simple objective function and minimal constraints. Our short position is one of the 13 at the money option selected by our sales desk. Our hedging universe is comprised of the other 104 options available for purchase and sale on the date of the hedge.
3. Lesson Three – Hedging Gamma and Vega – Solver Solution review
We review results from our Solver model and interpret them, evaluating the impact of changing constraints and objective functions. There are many ways to optimize and some are more “equal” than others.
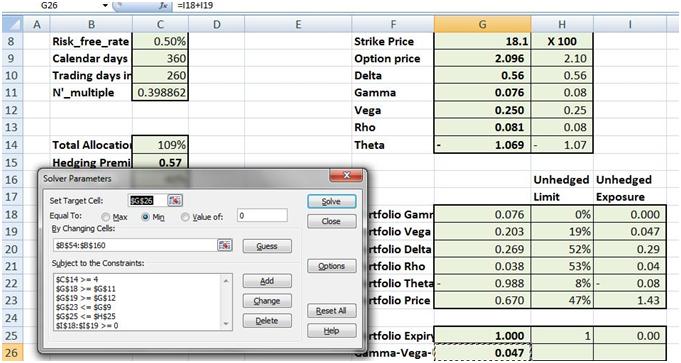
4. Lesson Four – Hedging Gamma and Vega for a book of options
What needs to change within the structure of the Solver model to hedge a book of written options rather than a single position. We introduce Vega and Gamma maturity buckets, Delta margins and new constraints on the number of open positions.
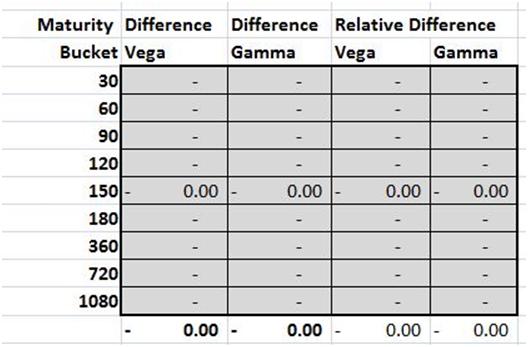
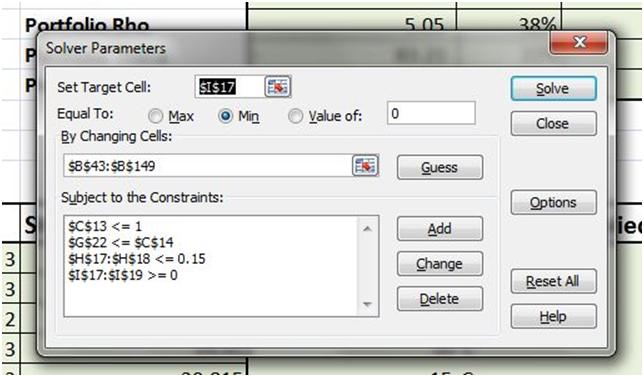
5. Lesson Five – Hedging Gamma and Vega exposure for portfolio of options – Solver solution review
The problem space is now revised to include a book of 13 options. We walk through a revised Solver model that handles Vega and Gamma buckets and evaluates solutions that minimize Delta, minimize hedge cost and minimize allocations (open positions) for the proposed hedging portfolio. We experiment with multiple objective functions to search for the one optimal solution.
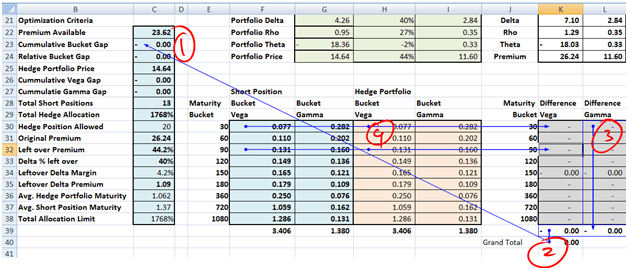
A review of hedge solutions (option allocations within our hedging universe) proposed by Excel solver point out obvious lessons. Shorter dated options are more sensitive to changes in the price of the underlying (Gamma) and less sensitive to changes in implied volatility (Vega). Longer dated options are more sensitive to changes in implied volatility. To find the optimal hedge solution you need to find the right balance between these two categories.
