Lesson Four – Hedging higher order Greeks for a book of short call options
We are now ready to move to a more sophisticated version of our hedging higher order Greeks problem. Rather than limiting ourselves to a single short position we are going to go ahead and sell multiple options.
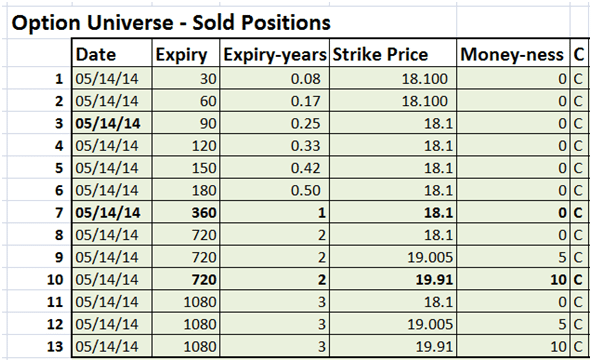
Here is an inventory of our short positions. We have sold 13 (for luck) at and near money options across maturities ranging from 30 days to 3 years. We now need to determine an acceptable approach that would allow us to hedge higher order Greeks for this book of short positions.
Figure 1 Book of short call positions – At and near money options
To hedge higher order Greeks we have the same universe of 104 call options that we had used in lesson three.
In our initial model we had used a single Gamma and Vega bucket because we only had a single short position with a single expiry. Given the fact that we have a range of maturities in our short portfolio and the fact that volatility varies across maturity buckets we would need to revise our approach by tracking Vega and Gamma exposure across maturity bucket. Our hedging strategy would also aim at ensuring that we track excess unhedged exposure by bucket as well as the Greek symbol in question.
In the Asset Liability Management, we are comfortable and familiar with the concept of tracking interest rate risk exposure by maturity buckets. We will use the same process here. The only difference is that rather than tracking interest rate sensitivity we would be tracking sensitivity to changes in implied volatility and the second order rate of change of the underlying spot price.
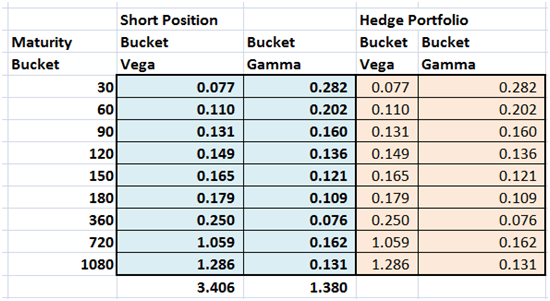
In an ideal world our methodology would allow us to match Gamma Vega exposure by maturity bucket across our original short position and our optimal hedge portfolio. Once our optimization process is complete we would be able to generate the table that would document the perfect match across buckets.
Figure 2 Building the Vega, Gamma maturity bucket
From an optimization point of view though given the complexity of this problem and Solver’s inherent limitations we still want to create a reasonable objective function that Excel can use to search for the optimal solution. So we use the grid created above to calculate absolute as well as relative difference by bucket and create an objective function using either of the two difference figures shown below.
Figure 3 Maturity differences by bucket grid for Vega, Gamma
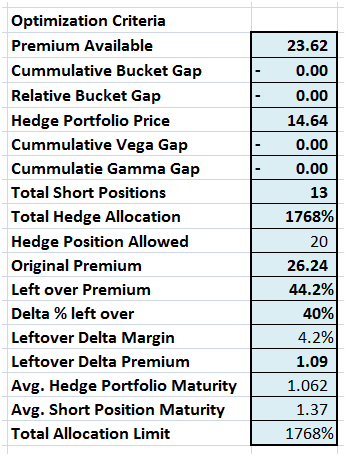
This obviously complicates our optimization criteria and the number of constraints we would need to add to help Solver reach an acceptable solution. Compared to our original criteria in lesson three, the revised optimization criteria has many more potential elements.
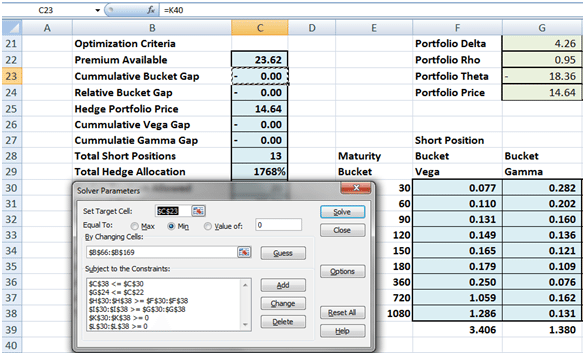
Figure 4 The new and improved optimization criteria
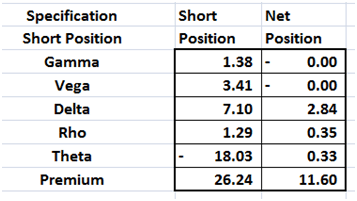
Once again as we saw earlier with our simpler model for a single short position, hedging higher order Greeks still leaves some exposure when it comes to Delta, Rho and Theta. The left over Delta exposure can be hedged using the Delta hedging approach we have covered earlier. Rho and Theta are minor Greeks that are managed through a limits and control process.
Figure 5 Net position after hedging Vega and Gamma
Based on our above discussion our Solver model is also different. The objective function has changed and now solves for minimizing the cumulative bucket gap. The constraints and conditions have been changed to accommodate multiple maturity buckets.
Figure 6 A glimpse of the solver model
We discuss creating the Solver model and running variations between possible solutions and constraints in our next post.


Comments are closed.